题目内容
【题目】如图①所示,直线L:y=mx+5m与x轴负半轴,y轴正半轴分别交于A、B两点.
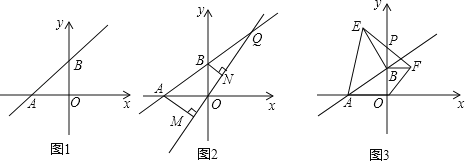
(1)当OA=OB时,求点A坐标及直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=4,求BN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)是,
;(3)是,![]()
【解析】
(1)由直线L解析式,求出![]() 与
与![]() 的坐标,根据
的坐标,根据![]() ,求出
,求出![]() 的值,即可确定出直线L解析式.
的值,即可确定出直线L解析式.
(2)由![]() ,对顶角相等,且一对直角相等,利用
,对顶角相等,且一对直角相等,利用![]() 得到
得到![]() ,用对应线段相等求长度;
,用对应线段相等求长度;
(3)如图,作![]() 轴于
轴于![]() 点,利用
点,利用![]() 得到
得到![]() ,利用全等三角形对应边相等得到
,利用全等三角形对应边相等得到![]() ,再利用
,再利用![]() 得到
得到![]() ,寻找相等线段,并进行转化,求
,寻找相等线段,并进行转化,求![]() 的长.
的长.
(1)∵直线L:![]() ,
,
∴![]() ,
,
由![]() ,得
,得![]() ,
,
∴直线L的解析式为:![]() ;
;
(2)![]()
∴![]()
又![]()
∴![]()
在△AMO与![]() 中,
中,
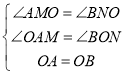 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
答案是:![]()
(3)如图,作![]() 轴于
轴于![]() 点,
点,
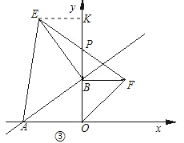
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() °,
°,
∴![]() °,
°,
∵![]() °,
°,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
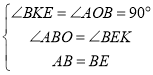 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
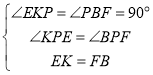 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目