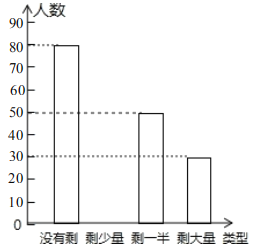
题目内容
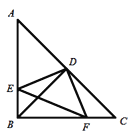
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 上取一点
上取一点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .交
.交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为________.
的长为________.

【答案】![]()
【解析】
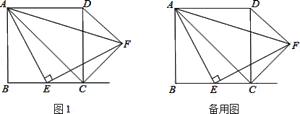
过B作BH⊥BC交DE的延长线于H,则BH∥AC,推出△ADE∽△BHE,根据相似三角形的性质得到![]() =
=![]() ,根据平行线的性质得到∠H=∠1,∠2=∠DBH,等量代换得到∠H=∠DBH,于是得到DH=BD,过D作DM⊥BH与M,根据等腰三角形的性质得到BM=
,根据平行线的性质得到∠H=∠1,∠2=∠DBH,等量代换得到∠H=∠DBH,于是得到DH=BD,过D作DM⊥BH与M,根据等腰三角形的性质得到BM=![]() BH=CD,设CD=x,则BH=2x,根据余角的性质得到∠2=∠3,推出△ADE∽△BFE,根据相似三角形的性质即可得到结论.
BH=CD,设CD=x,则BH=2x,根据余角的性质得到∠2=∠3,推出△ADE∽△BFE,根据相似三角形的性质即可得到结论.
过B作BH⊥BC交DE的延长线于H,则BH∥AC,
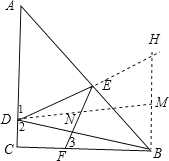
∴△ADE∽△BHE,
∴![]() =
=![]() ,
,
∵BH∥AC,
∴∠H=∠1,∠2=∠DBH,
∵∠1=∠2,
∴∠H=∠DBH,
∴DH=BD,
过D作DM⊥BH与M,
∴BM=![]() BH=CD,设CD=x,则BH=2x,
BH=CD,设CD=x,则BH=2x,
∵EF⊥BD,
∴∠BNF=90°,
∴∠2+∠CBD=∠3+∠NBF,
∴∠2=∠3,
∵∠A=∠FBE=45°,
∴∠1=∠3,
∴△ADE∽△BFE,
∴![]() =
=![]() =
=![]() ,
,
∴BF=BH,即11+x8=2x,
∴x=3.
∴CD=3.
故答案为:3.

练习册系列答案
相关题目