Question

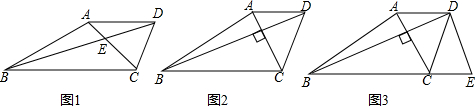
8．【提出问题】如图①，在梯形ABCD中，AD∥BC，AC、BD交于点E，∠BEC=n°，若AD=a，BC=b，则梯形ABCD的面积最大是多少？
【探究过程】小明提出：可以从特殊情况开始探究，如图②，在梯形ABCD中，AD∥BC，AC⊥BD，若AD=3，BC=7，则梯形ABCD的面积最大是多少？
如图③，过点D做DE∥AC交BC的延长线于点E，那么梯形ABCD的面积就等于△DBE的面积，求梯形ABCD的面积最大值就是求△DBE的面积最大值．如果设AC=x，BD=y，那么S_△DBE=$\frac{1}{2}$xy．
以下是几位同学的对话：
A同学：因为y=$\sqrt{100-{x}^{2}}$，所以S_△DBE=$\frac{1}{2}$x$\sqrt{100-{x}^{2}}$，求这个函数的最大值即可．
B同学：我们知道x²+y²=100，借助完全平方公式可求S_△DBE=$\frac{1}{2}$xy的最大值
C同学：△DBE是直角三角形，底BE=10，只要高最大，S_△DBE就最大，我们先将所有满足BE=10的直角△DBE都找出来，然后在其中寻找高最大的△DBE即可．
（1）请选择A同学或者B同学的方法，完成解题过程．
（2）请帮C同学在图③中画出所有满足条件的点D，并标出使△DBE面积最大的点D₁．（保留作图痕迹，可适当说明画图过程）
【解决问题】根据对特殊情况的探究经验，请在图①中画出面积最大的梯形ABCD的顶点D₁，并直接写出梯形ABCD面积的最大值．

Answer 1

分析 （1）A同学：化成顶点式，即可得出答案；B同学：根据完全平方公式变形，再求出最值即可；
（2）过B、D、E三点作圆，作BF的垂直平分线交圆于点D₁，即可得出答案；过B、D、F三点作圆，作BF的垂直平分线即可．

解答 解：（1）选择A同学：
S_△DBE=$\frac{1}{2}$x$\sqrt{100-{x}^{2}}$=$\frac{1}{2}$$\sqrt{100{x}^{2}-{x}^{4}}$=$\frac{1}{2}$$\sqrt{-（{x}^{2}-50）^{2}+2500}$，
当x²=50，即x=5$\sqrt{2}$，S_△DBE取最大值25；
选择B同学．
方法一：S_△DBE=$\frac{1}{2}$xy=$\frac{1}{4}$×2xy≤$\frac{1}{4}$（x²+y²）=25，
当x=y=5$\sqrt{2}$时，S_△DBE取最大值25；
方法二：S_△DBE=$\frac{1}{2}$xy=$\frac{1}{4}$[（x²+y²）-（x-y）²]=$\frac{1}{4}$[100-（x-y）²]，
当（x-y）²=0，即x=y=5$\sqrt{2}$时，S_△DBE取最大值25；

（2）如图：
点D₁即为所求的点；
如图：

如图2，
设BF的垂直平分线交⊙O于D₁，M，交BF于N，连接BM、FM，FO，BO，
∵AC∥DF，
∴∠BDF=∠BEC=n°，
则∠BMF=180°-n°，
由圆周角定理得：∠BOF=2∠BMP=360°-2n°，
∵OB=OF，NM⊥BF，
∴BN=FN=$\frac{1}{2}$（a+b），∠BON=$\frac{1}{2}$∠BOF=180°-n°，
在Rt△BNO中，ON=$\frac{BN}{tan（180°-n°）}$=$\frac{\frac{1}{2}（a+b）}{tan（180°-n°）}$，
OD₁=OB=$\frac{BN}{sin（180°-n°）}$=$\frac{\frac{1}{2}（a+b）}{sin（180°-n°）}$，
∴D₁N=D₁O-ON=$\frac{\frac{1}{2}（a+b）}{sin（180°-n°）}$-$\frac{\frac{1}{2}（a+b）}{tan（180°-n°）}$，
∴S_梯形ABCD=$\frac{1}{2}$（AD₁+BC）×D₁N
=$\frac{1}{2}$（a+b）[$\frac{\frac{1}{2}（a+b）}{sin（180°-n°）}$-$\frac{\frac{1}{2}（a+b）}{tan（180°-n°）}$]
=$\frac{（a+b）^{2}}{4sinn°tann°}$
S_梯形ABCD最大值为：$\frac{（a+b）^{2}}{4sinn°tann°}$．

点评 本题考查了三角形的外接圆，三角形的面积，完全平方公式，二次函数的最值，平行四边形的性质和判定，梯形的性质的应用，主要考查学生的动手操作能力和理解能力，难度偏大．此类问题是初中数学的重点和难点，在中考中极为常见，一般以压轴题形式出现，难度较大．此类问题是初中数学的重点和难点，在中考中极为常见，一般以压轴题形式出现，难度较大．