题目内容
3.在△ABC中,∠C=90°,AC=4,BC=3,把它绕AC旋转一周得一几何体,该几何体的表面积为( )| A. | 24π | B. | 21π | C. | 16.8π | D. | 36π |
分析 以直线AC为轴旋转一周所得到的几何体的表面积是一圆锥的侧面积加底面积,根据圆锥的侧面积公式计算即可.
解答 解:根据题意得:圆锥的底面周长=6π,
所以圆锥的侧面积=$\frac{1}{2}$×6π×5=15π,
圆锥的底面积=π×32=9π,
所以以直线AC为轴旋转一周所得到的几何体的表面积=15π+9π=24π.
故选A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了扇形的面积公式.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.计算:(-2)+3的结果是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
14. 如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
 如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
8. 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )
 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
15.2的算术平方根是( )
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 2 |
12.-22=( )
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
13.cos60°的值等于( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
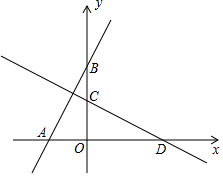 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.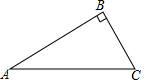 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$.
如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$.