题目内容
已知:抛物线经过A(0,1),B(2,-7),C(-3,-2).
(1)求抛物线的解析式;
(2)抛物线与直线y=-x+k有且只有一个公共点,求k的值.
(1)求抛物线的解析式;
(2)抛物线与直线y=-x+k有且只有一个公共点,求k的值.
考点:待定系数法求二次函数解析式,根的判别式
专题:计算题
分析:(1)设一般式,利用待定系数法求抛物线解析式;
(2)把抛物线与直线有且只有一个公共点的问题转化为方程组只有一组解,然后把方程组的解问题转化为一元二次方程根的问题,再利用根的判别式的意义解决问题.
(2)把抛物线与直线有且只有一个公共点的问题转化为方程组只有一组解,然后把方程组的解问题转化为一元二次方程根的问题,再利用根的判别式的意义解决问题.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,
根据题意得
,
解得
.
所以抛物线解析式为y=-x2-2x+1;
(2)根据题意方程组
只有一组解,
所以-x2-2x+1=-x+k有相等的两实数解,
整理得x2+x+k-1=0,
所以△=12-4(k-1)=0,
解得k=
.
根据题意得
|
解得
|
所以抛物线解析式为y=-x2-2x+1;
(2)根据题意方程组
|
所以-x2-2x+1=-x+k有相等的两实数解,
整理得x2+x+k-1=0,
所以△=12-4(k-1)=0,
解得k=
| 5 |
| 4 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列说法中正确的是( )
| A、a和0都是单项式 | ||
| B、多项式-3a2b+7a2b2-2ab+l的次数是3 | ||
C、单项式-
| ||
| D、x2+2xy-y2可读作x2、2xy、y2的和 |
 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题: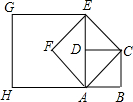 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,则an=
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,则an=