题目内容
5. 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.(1)过三角形的三个顶点有三条面积等分线,平行四边形有无数条面积等分线;
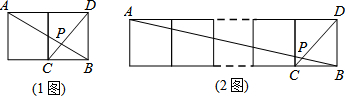
(2)如图所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线,并说明理由.
分析 (1)读懂面积等分线的定义,得出三角形的面积等分线;平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线;
(2)由(1)知,矩形的一条对角线所在的直线就是矩形的一条面积等分线.
解答 解:(1)在△ABC中,作BC的中线AD,因此直线AD将△ABC分成了面积相等的两部分,是三角形的面积等分线.因此,按这样的做法,可以作三条三角形的面积等分线;对于平行四边形应该有无数条,只要过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分.
故答案是:三;无数;
(2)如图2所示:连接2个矩形的对角线的交点的直线即把这个图形分成2个相等的部分.即OO′为这个图形的一条面积等分线,直线O1O2即是其中的一条;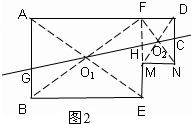
理由:如图∵FE∥AB,
∴∠AGO1=∠EHO1,
∠GAO1=∠HEO1,
而O1A=O1E,
∴△AGO1≌△EHO1,
∴AG=EH,
同理可证:GB=HF,
∴梯形AGHF面积=梯形EHGB面积,
同样有梯形DCHF面积=梯形HMNC面积,
∴直线O1O2即是该图形的面积等分线.
点评 本题考查了学生的阅读理解能力、运用作图工具的能力,以及运用三角形、等底等高性质等基础知识解决问题的能力都有较高的要求.还渗透了由“特殊”到“一般”的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知点A(1,2),O是坐标原点,将线段OA绕点O逆时针旋转90°,点A旋转后的对应点是A1,则点A1的坐标是( )
| A. | (-2,1) | B. | (2,-1) | C. | (-1,2) | D. | (-1,-2) |
14.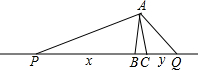 如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
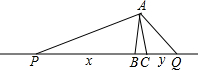 如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )| A. | 当x≠y时,△APB≌△AQC | B. | 当x=y时,∠APB=∠PAB=45° | ||
| C. | 当x=2y时,$\frac{AP}{AQ}$=$\sqrt{2}$ | D. | 当x•y=4时,AB=4 |

 如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).
如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).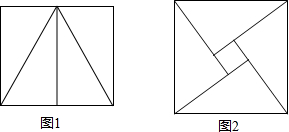 小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长
小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长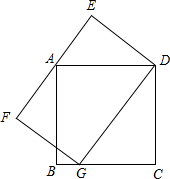 已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.
已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.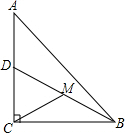 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.
如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.