题目内容
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是弦
是弦![]() 的中点,
的中点,![]() 是
是![]() 外一点且
外一点且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
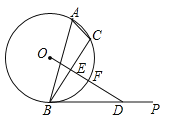
(1)求证:![]() 是
是![]() 的切线
的切线
(2)若![]() 的半径为6,
的半径为6,![]() 求弦
求弦![]() 的长.
的长.
【答案】(1)证明见解析;(2)9.6.
【解析】
(1)如下图,连接OB,根据点E是BC的中点,可推导得到∠BOE=∠A,从而得到∠BOE=∠PBC,最终得出∠OBE+∠PBC=90°;
(2)在Rt△OBD中,可求得OD的长,在△OBD中,分别以BD和OD为底求面积,根据面积相等得到BE的长.
(1)证明:如图,连接OB
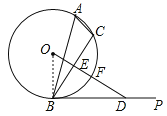
∵E是弦BC的中点,
∴BE=CE,OE⊥BC,![]() =
=![]() =
=![]()
![]()
∴∠BOE=∠A,∠OBE+∠BOE=90°
∵∠PBC=∠A,
∴∠BOE=∠PBC
∴∠OBE+∠PBC=90°即BP⊥OB
∴BP是⊙O的切线
(2)解:∵OB=6,BD=8,BD⊥OB
∴OD=![]() =10
=10
∵OBD的面积=![]() OD·BE=
OD·BE=![]() OB·BD,
OB·BD,
∴BE=![]() =
=![]() =4.8
=4.8
∴BC=2BE=9.6

练习册系列答案
相关题目