题目内容
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于65元,市场调查发现,若每箱以50元的价格出售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与涨价x(元/箱)之间的函数关系式;
(2)求当每箱苹果的销售价为多少元,批发商平均每天的销售利润W(元)可以获得最大?
(1)求平均每天销售量y(箱)与涨价x(元/箱)之间的函数关系式;
(2)求当每箱苹果的销售价为多少元,批发商平均每天的销售利润W(元)可以获得最大?
考点:二次函数的应用
专题:
分析:(1)根据每天的销量=原来的销量-每天减少的销量就可以得出售量y(箱)与涨价x(元/箱)之间的函数关系式;
(2)销售利润w(元)=每箱的销售利润×每天的销售量,根据题中所给的自变量的取值得到二次的最值问题即可.
(2)销售利润w(元)=每箱的销售利润×每天的销售量,根据题中所给的自变量的取值得到二次的最值问题即可.
解答:解:(1)y=90-3x;
(2)W=(x+50-40)(90-3x)
=-3x2+60x+900,
∵-3<0
∴抛物线开口向下.
当x=-
=10时,y有最大值.
∴当售价为50+10=60元时,y的最大值为600元.
∴当每箱苹果的销售价为60元时,可以获得600元的最大利润.
(2)W=(x+50-40)(90-3x)
=-3x2+60x+900,
∵-3<0
∴抛物线开口向下.
当x=-
| b |
| 2a |
∴当售价为50+10=60元时,y的最大值为600元.
∴当每箱苹果的销售价为60元时,可以获得600元的最大利润.
点评:此题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常用函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
下列说法正确的是( )
| A、用一个平面去截正方体能得到八边形 |
| B、用一个平面去截长方体能得到七边形 |
| C、用一个平面去截圆柱能得到梯形 |
| D、用一个平面去截圆柱能得到四边形 |
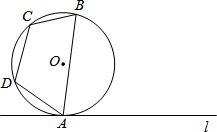 如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°,
如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°, |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC的三边长分别为1、5、x,周长为整数,则△ABC的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
下列长度的各组线段中,能组成三角形的是( )
| A、5cm,9cm,3cm |
| B、3cm,11cm,8cm |
| C、6.3cm,6.3cm,4.4cm |
| D、15cm,8cm,6cm |
以下事件中不可能事件是( )
| A、一个角和它的余角的和是90° |
| B、连接掷10次骰子都是6点朝上 |
| C、一个有理数与它的倒数之和等于0 |
| D、一个有理数小于它的倒数 |
 如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( )
如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( )