题目内容
以AB为直径作半圆O,AB=10,点C是该半圆上一动点,连接AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,连接OF.
(1)如图①,当点E与点O重合时,求∠BAC的度数;
(2)如图②,当DE=8时,求线段EF的长;
(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似?若存在,请直接写出此时线段OE的长;若不存在,请说明理由.

(1)如图①,当点E与点O重合时,求∠BAC的度数;
(2)如图②,当DE=8时,求线段EF的长;
(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似?若存在,请直接写出此时线段OE的长;若不存在,请说明理由.

分析:(1)连接OC.根据直角三角形的性质和圆的性质可得△OBC是等边三角形,再根据等边三角形的性质和直角三角形两锐角互余即可得到∠BAC的度数;
(2)连接DA.根据垂直平分线的性质可得AB=AD=10,根据勾股定理和线段的和差关系可得AE和BE的长,通过AA证明△AEF∽△DEB,根据相似三角形的性质即可得到EF的长;
(3)分两种情况:①当交点E在O、A之间时;②当交点E在O、B之间时;讨论即可求得线段OE的长.
(2)连接DA.根据垂直平分线的性质可得AB=AD=10,根据勾股定理和线段的和差关系可得AE和BE的长,通过AA证明△AEF∽△DEB,根据相似三角形的性质即可得到EF的长;
(3)分两种情况:①当交点E在O、A之间时;②当交点E在O、B之间时;讨论即可求得线段OE的长.
解答: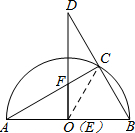 解:(1)连接OC.
解:(1)连接OC.
∵C为DB中点,
∴OC=BC=OB,
∴△OBC是等边三角形,
∴∠B=60°,
∵AB为直径,
∴∠ACB=90°,
∴∠BAC=30°;
(2)连接DA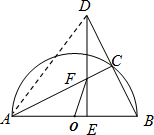 .
.
∵AC垂直平分BD,
∴AB=AD=10,
∵DE=8,DE⊥AB,
∴AE=6,
∴BE=4,
∵∠FAE+∠AFE=90°,∠CFD+∠CDF=90°,
∴∠CDF=∠EAF,
∵∠AEF=∠DEB=90°,
∴△AEF∽△DEB,
∴
=
,
∴EF=3;
(3)①当交点E在O、A之间时,
若∠EOF=∠BAC,此时
=
,则OE=
;
若∠EOF=∠ABC,此时
=
,则OE=
;
②当交点E在O、B之间时,OE=
.
综上所述,OE=
或
或
.
 解:(1)连接OC.
解:(1)连接OC.∵C为DB中点,
∴OC=BC=OB,
∴△OBC是等边三角形,
∴∠B=60°,
∵AB为直径,
∴∠ACB=90°,
∴∠BAC=30°;
(2)连接DA
 .
.∵AC垂直平分BD,
∴AB=AD=10,
∵DE=8,DE⊥AB,
∴AE=6,
∴BE=4,
∵∠FAE+∠AFE=90°,∠CFD+∠CDF=90°,
∴∠CDF=∠EAF,
∵∠AEF=∠DEB=90°,
∴△AEF∽△DEB,
∴
| EF |
| EB |
| AE |
| DE |
∴EF=3;
(3)①当交点E在O、A之间时,
若∠EOF=∠BAC,此时
| OE |
| AC |
| EF |
| BC |
| 5 |
| 3 |
若∠EOF=∠ABC,此时
| OE |
| BC |
| EF |
| AC |
| 5 |
| 2 |
②当交点E在O、B之间时,OE=
-15+5
| ||
| 4 |
综上所述,OE=
| 5 |
| 2 |
| 5 |
| 3 |
-15+5
| ||
| 4 |
点评:考查了圆的综合题,涉及的知识点有直角三角形的性质和圆的性质,等边三角形的判定和性质,垂直平分线的性质,勾股定理,相似三角形的判定和性质,分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
相关题目
 接OE,并延长交AD的延长线于F.
接OE,并延长交AD的延长线于F. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D.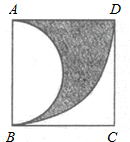 (2011•巴中)已知如图所示,正方形ABCD的边长为1,以AB为直径作半圆,以点A为圆心,AD为半径画弧.那么图中阴影部分的面积为
(2011•巴中)已知如图所示,正方形ABCD的边长为1,以AB为直径作半圆,以点A为圆心,AD为半径画弧.那么图中阴影部分的面积为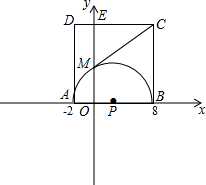 如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆⊙P交y轴于M,以AB为一边作正方形ABCD.
如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆⊙P交y轴于M,以AB为一边作正方形ABCD.