题目内容
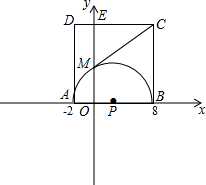 如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆⊙P交y轴于M,以AB为一边作正方形ABCD.
如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆⊙P交y轴于M,以AB为一边作正方形ABCD.(1)求C、M两点的坐标;
(2)连CM,试判断直线CM是否与⊙P相切?说明你的理由.
(3)在x轴上是否存在一点Q,使△QMC周长最小?若存在,求出Q的坐标及△QMC最小周长;若不存在.请说明理由.
分析:(1)利用正方形的性质得出BC=AB=10,得出C点坐标,进而利用勾股定理求出OM的长,即可得出答案;
(2)利用已知得出,CM2+MP2=CP2,即可得出CM与⊙P相切;
(3)利用轴对称性质得出Q点的位置,进而利用勾股定理求出答案.
(2)利用已知得出,CM2+MP2=CP2,即可得出CM与⊙P相切;
(3)利用轴对称性质得出Q点的位置,进而利用勾股定理求出答案.
解答: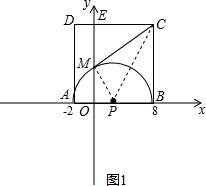 解:(1)∵A(-2,0),B(8,0),
解:(1)∵A(-2,0),B(8,0),
∴AB=10.
∵四边形ABCD为正方形,
∴BC=AB=10,
∴C(8,10).
连接MP
在Rt△OPM中,OP=3,MP=5,
∴OM=4,即M(0,4);
(2)CM与⊙P相切,
理由:连接PC,在Rt△CBP中,CB=10,BP=5,
∴CP2=125.
在Rt△CEM中,EM=6,CE=8,
∴CM2=100.
∵100+25=125,
∴△CMP中,CM2+MP2=CP2,
∴∠CMP=90°.
即:PM⊥CM.
∴CM与⊙P相切.
(3)△QMC中,CM恒等于10,要使△QMC周长最小,即要使MQ+QC最小.
故作M关于x轴对称点M′,连CM′交x轴于点Q,连MQ,此时,△QMC周长最小.
∵C(8,10),M′(0,-4),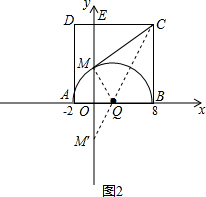
设直线CM′:y=kx+b(k≠0)
∴
,
∴
,
∴y=
x-4,
当y=0时,x=
,
∴Q(
,0)
∵x轴垂直平分MM′,
∴QM=QM′,
∴MQ+QC=M'Q+QC=M′C.
在Rt△CEM′中,CE=8,EM′=14,
∴CM′=2
,MC=10,
∴△QMC周长最小值为:2
+10.
∴存在符合题意的点,此时△QMC周长最小值为2
+10.
 解:(1)∵A(-2,0),B(8,0),
解:(1)∵A(-2,0),B(8,0),∴AB=10.
∵四边形ABCD为正方形,
∴BC=AB=10,
∴C(8,10).
连接MP
在Rt△OPM中,OP=3,MP=5,
∴OM=4,即M(0,4);
(2)CM与⊙P相切,
理由:连接PC,在Rt△CBP中,CB=10,BP=5,
∴CP2=125.
在Rt△CEM中,EM=6,CE=8,
∴CM2=100.
∵100+25=125,
∴△CMP中,CM2+MP2=CP2,
∴∠CMP=90°.
即:PM⊥CM.
∴CM与⊙P相切.
(3)△QMC中,CM恒等于10,要使△QMC周长最小,即要使MQ+QC最小.
故作M关于x轴对称点M′,连CM′交x轴于点Q,连MQ,此时,△QMC周长最小.
∵C(8,10),M′(0,-4),

设直线CM′:y=kx+b(k≠0)
∴
|
∴
|
∴y=
| 7 |
| 4 |
当y=0时,x=
| 16 |
| 7 |
∴Q(
| 16 |
| 7 |
∵x轴垂直平分MM′,
∴QM=QM′,
∴MQ+QC=M'Q+QC=M′C.
在Rt△CEM′中,CE=8,EM′=14,
∴CM′=2
| 65 |
∴△QMC周长最小值为:2
| 65 |
∴存在符合题意的点,此时△QMC周长最小值为2
| 65 |
点评:此题主要考查了勾股定理的应用以及利用轴对称求最小值问题和待定系数法求一次函数解析式等知识,根据已知得出对称点Q的位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.