题目内容
6．
已知：如图，在△ABC，AB=AC，AD是BC边上的中线，E是AC的中点，BF⊥CA延长线于点F．求证：∠CBF=∠ADE．
分析 由等腰三角形的性质及在直角三角形中，斜边上的中线等于斜边的一半的性质可得：∠ADE=∠EAD=90°-∠C，又因为∠CBF=90°-∠C，进而可证明∠CBF=∠ADE．
解答 证明：
∵AB=AC，AD是BC边上的中线，
∴∠ADC=90°，
又∵E是AC的中点，
∴AE=DE，
∴∠ADE=∠EAD=90°-∠C，
∵BF⊥CA延长线于点F，
∴∠CBF=90°-∠C，
∴∠CBF=∠ADE．
点评 本题考查了在直角三角形中，斜边上的中线等于斜边的一半的性质以及等腰三角形的性质，熟记各种和特殊三角形有关的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
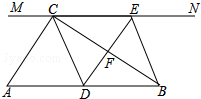如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（结果保留根号）
如图，已知AB=AC=AD，且AD∥BC，求证：∠DAC=2∠D．
如图，已知点E、C在线段BF上，且BE=CF，CM∥DF，
如图，线段AB=16，以AB为直径的半圆上有一点C，连接BC并延长到点D，使DC=2BC，连接OD、AC交于点E，当∠B=2∠D时，线段OE的长为$\frac{4\sqrt{10}}{5}$．
如图，等边三角形ABC内接于半径为1的⊙O，以BC为一边作⊙O的内接矩形BCDE，则矩形BCDE的面积为$\sqrt{3}$．