Question

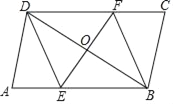
【题目】如图，在等腰中，，是斜边的中点，交边、于点、，连结，且，若，，则的面积是( )

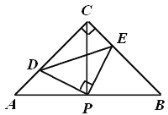
A.2B.2.5C.3D.3.5

Answer 1

【答案】B

【解析】

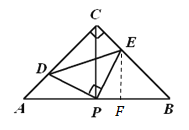
首先根据等腰直角三角形的性质和余角的性质可证明△BPE≌△CPD，可得PE=PD，于是所求的的面积即为，故只要求出PE2的值即可，可过点E作EF⊥AB于点F，如图，根据题意可依次求出BE、BF、BP、PF的长，即可根据勾股定理求出PE2的值，进而可得答案．

解：在中，∵，AC=BC，是斜边的中点，

∴AP=BP=CP，CP⊥AB，∠B=∠BCP=∠DCP=45°，

∵∠DPC+∠EPC=90°，∠BPE+∠EPC=90°，∴∠DPC=∠BPE，

在△BPE和△CPD中，∵∠B=∠DCP，BP=CP，∠BPE=∠DPC，∴△BPE≌△CPD（ASA），

∴PE=PD，

∵，，∴CE=1，BE=3，

过点E作EF⊥AB于点F，如图，则EF=BF=，

又∵BP=，∴，

在直角△PEF中，，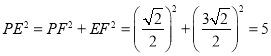

∴的面积=．

故选：B．