题目内容
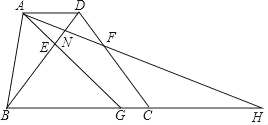
【题目】如图.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中位线,连结
的中位线,连结![]() ,点
,点![]() 是边
是边![]() 上的一个动点,连结
上的一个动点,连结![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值及
的值及![]() 的长
的长
(2) 当四边形![]() 与四边形
与四边形![]() 的面积相等时,求
的面积相等时,求![]() 的长:
的长:
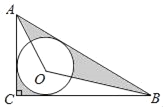
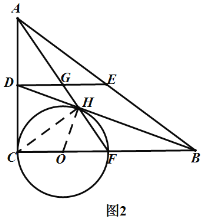
(3)如图2.以![]() 为直径作
为直径作![]() .
.
①当![]() 正好经过点
正好经过点![]() 时,求证:
时,求证:![]() 是
是![]() 的切线:
的切线:
②当![]() 的值满足什么条件时,
的值满足什么条件时,![]() 与线段
与线段![]() 有且只有一个交点.
有且只有一个交点.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)①见解析;②当
;(3)①见解析;②当![]() 或
或![]() 时,
时,![]() 与线段
与线段![]() 有且只有一个交点.
有且只有一个交点.
【解析】
(1)根据题意得H为![]() 的重心,即可得
的重心,即可得![]() 的值,由重心和中位线的性质求得
的值,由重心和中位线的性质求得![]() ,由勾股定理求得
,由勾股定理求得![]() 的长,即可得
的长,即可得![]() 的长;
的长;
(2)根据图中面积的关系得S四边形DCFG=![]() ,列出关系式求解即可得
,列出关系式求解即可得![]() 的长;
的长;
(3)根据![]() 与线段
与线段![]() 有且只有一个交点,可分两类情况讨论:当
有且只有一个交点,可分两类情况讨论:当![]() 与
与![]() 相切时,求得
相切时,求得![]() 的值;当
的值;当![]() 过点E,此时是
过点E,此时是![]() 与线段
与线段![]() 有两个交点的临界点,即可得出
有两个交点的临界点,即可得出![]() 与线段
与线段![]() 有且只有一个交点时
有且只有一个交点时![]() 满足的条件.
满足的条件.
解:(1)∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,
又∵点![]() 是
是![]() 的中点,
的中点,
∴![]() 与
与![]() 的交点
的交点![]() 是
是![]() 的重心,
的重心,
![]() ,即
,即![]() ;
;![]() ,
,
∴![]() ,
,
在![]() 中,D为AC中点,
中,D为AC中点,![]() ,则
,则![]() ,
,
∴DG为![]() 的中位线,G为AF的中点,
的中位线,G为AF的中点,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,
![]() ;
;
(2)∵四边形![]() 与四边形
与四边形![]() 的面积相等,
的面积相等,
∴S四边形DCFH+![]() =S四边形BEGH+
=S四边形BEGH+![]() ,
,
即S梯形DCFG=![]() ,
,
∵![]() ,
,![]() ,
,![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∵![]() ,
,
设![]() ,∵DG为
,∵DG为![]() 的中位线,
的中位线,
∴![]() ,
,
则S梯形DCFG![]() ,
,
解得:![]() ,
,
![]() ;
;
(3)①证明:如图2,连结![]() ,
,
![]() 为
为![]() 的直径,
的直径,![]() 经过点
经过点![]() ,
,
![]() ,
,
∴![]() ,
,![]() 为直角三角形,
为直角三角形,
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() 是
是![]() 的切线;
的切线;
②如图3-1,当![]() 与
与![]() 相切时,
相切时,![]() 与线段
与线段![]() 有且只有一个交点,
有且只有一个交点,
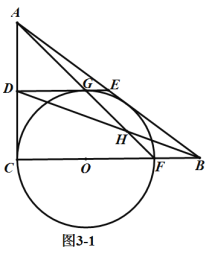
设![]() 的半径为r,圆心O到DE的距离为d,
的半径为r,圆心O到DE的距离为d,
∴当r=d时,![]() 与
与![]() 相切,
相切,
∵![]() ,
,![]() ,
,![]() ,
,
∴两平行线![]() 之间的距离为
之间的距离为![]() ,
,
∴![]() ,
,
则![]() ,
,![]() ,
,
由![]() 得:
得:![]() ,
,
![]() ;
;
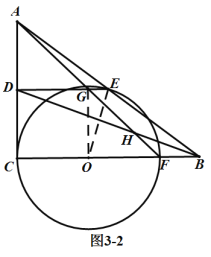
如图3-2,当![]() 经过点
经过点![]() 时,连接
时,连接![]() 、
、![]() ,
,
设![]() 的半径为
的半径为![]() ,即
,即![]() ,
,
∵G为AF的中点,O为CF的中点,
∴![]() ,
,
∴四边形COGD为平行四边形,
又∵![]() ,
,
∴四边形COGD为矩形,
∴![]() ,则
,则![]() ,
,![]() 为直角三角形,
为直角三角形,
∴![]() ,
,![]() ,
,
则![]() ,
,
由勾股定理得:![]() ,即
,即![]() ,
,
解得:![]() ,则
,则![]() ,
,![]()
![]() ,
,
由![]() 得:
得:![]() ,
,
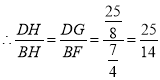 ,
,
则当![]() 时,
时,![]() 与线段
与线段![]() 有且只有一个交点;
有且只有一个交点;
综上所述,当![]() 或
或![]() 时,
时,![]() 与线段
与线段![]() 有且只有一个交点.
有且只有一个交点.