题目内容
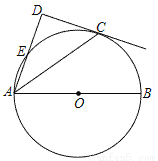
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=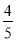 ,求
,求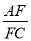 的值.
的值.
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
题目内容
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=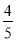 ,求
,求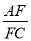 的值.
的值.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案