题目内容
直线y=kx-4与y轴相交所成锐角的正切值为 ,则k的值为
,则k的值为
- A.

- B.2
- C.±2
- D.

C
分析:首先确定直线y=kx-4与y轴和x轴的交点,然后利用直线y=kx-4与y轴相交所成锐角的正切值为 这一条件求出k的值.
这一条件求出k的值.
解答:由直线的解析式可知直线与y轴的交点为(0,-4),即直线y=kx-4与y轴相交所成锐角的邻边为|-4|=4,与x轴的交点为y=0时,x=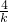 ,
,
∵直线y=kx-4与y轴相交所成锐角的正切值为 ,
,
即|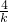 |=4×
|=4× ,k=±2.
,k=±2.
故选C.
点评:此题比较复杂,涉及到锐角三角函数,在解题时要注意k的正负.
分析:首先确定直线y=kx-4与y轴和x轴的交点,然后利用直线y=kx-4与y轴相交所成锐角的正切值为
 这一条件求出k的值.
这一条件求出k的值.解答:由直线的解析式可知直线与y轴的交点为(0,-4),即直线y=kx-4与y轴相交所成锐角的邻边为|-4|=4,与x轴的交点为y=0时,x=
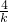 ,
,∵直线y=kx-4与y轴相交所成锐角的正切值为
 ,
,即|
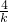 |=4×
|=4× ,k=±2.
,k=±2.故选C.
点评:此题比较复杂,涉及到锐角三角函数,在解题时要注意k的正负.

练习册系列答案
相关题目
已知直线y=kx+b与双曲线y=
交于(x1,y1)、(x2,y2)两点,则x1x2的值( )
| k |
| x |
| A、与k有关,与b无关 |
| B、与k无关,与b有关 |
| C、与k、b都无关 |
| D、与k、b都有关 |
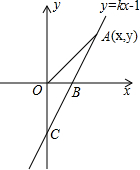 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB=
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB= 12、如图,直线y1=kx+b与y2=-x-1交于点P,它们分别与x轴交于A、B,且B、P、A三点的横坐标分别为-1,-2,-3,则满足y1>y2的x的取值范围是
12、如图,直线y1=kx+b与y2=-x-1交于点P,它们分别与x轴交于A、B,且B、P、A三点的横坐标分别为-1,-2,-3,则满足y1>y2的x的取值范围是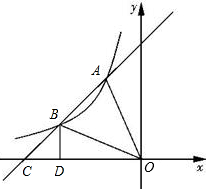 点C,过B作BD⊥x轴,且S△OBD=4,其中点A的坐标为(n,4),点B的坐标为(-4,m)
点C,过B作BD⊥x轴,且S△OBD=4,其中点A的坐标为(n,4),点B的坐标为(-4,m)