题目内容
10.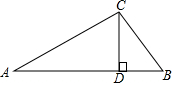 有一种屋顶的截面形状为三角形(如图),从屋子的最高处C点立一条垂直于横梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形吗?说明理由.
有一种屋顶的截面形状为三角形(如图),从屋子的最高处C点立一条垂直于横梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形吗?说明理由.
分析 在Rt△BCD中,先求出CD的长,然后在Rt△ACD中可求出AD的长;再根据勾股定理的逆定理可得出答案.
解答 解:在Rt△BCD中可得,CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=12,
∴在Rt△ACD中可得AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=16.
∴AB=BD+DA=25,
∴AB2=AC2+BC2,
∴△ABC是直角三角形.
点评 此题主要考查了勾股定理和勾股定理逆定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
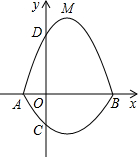 如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.
如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.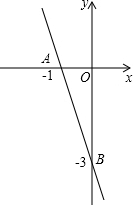 已知:点A(-1,0),B(0,-3).
已知:点A(-1,0),B(0,-3).