题目内容
如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是( )
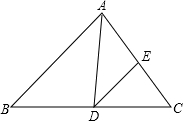
A．45° B．54° C．40° D．50°
C【考点】平行线的性质；三角形内角和定理．
【分析】根据三角形的内角和定理求出∠BAC，再根据角平分线的定义求出∠BAD，然后根据两直线平行，内错角相等可得∠ADE=
∠BAD．
【解答】解：∵∠B=46°，∠C=54°，
∴∠BAC=180°﹣∠B﹣∠C=180°﹣46°﹣54°=80°，
∵AD平分∠BAC，
∴∠BAD=
∠BAC=×80°=40°，
∵DE∥AB，
∴∠ADE=∠BAD=40°．
故选：C．
【点评】本题考查了平行线的性质，三角形的内角和定理，角平分线的定义，熟记性质与概念是解题的关键．
练习册系列答案
相关题目
×[3﹣（﹣3）2]树的高度与树生长的年数有关，测得某棵树的有关数据如下表（树苗原高8
0厘米）：
| 年数a | 高度h（单位：厘米） |
| 1 | 87 |
| 2 | 94 |
| 3 | 101 |
| 4 | __________ |
| … | … |
（1）填出第4年树苗可能达到的高度；
（2）请用含a的代数式表示：a年后树的高度h=__________；
（3）根据这种长势，12年后这棵树可能达到的高度是__________厘米．
们在用“☆”定义一种新运算：对于任意有理数a和正整数n．
，例如：（﹣3）☆2=
=
=﹣3．