Question

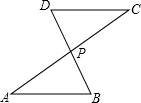如图，AC与BD交于点P，AP=CP，从以下四个论断①AB=CD，②BP=DP，③∠B=∠D，④∠A=∠C中选择一个论断作为条件，则不一定能使△APB≌△CPD的论断是

 

（限填序号）．

Answer 1

考点：全等三角形的判定

专题：

分析：根据全等三角形的判定方法：SSS、SAS、ASA、AAS、HL，进行解答．

解答：解：①∵SSA不能判定两个三角形全等，
∴AB=CD不能使△APB≌△CPD；
②在△APB和△CPD中，

BP=DP ∠DPC=∠BPA AP=CP

，
∴△APB≌△CPD（SAS）；
③在△APB和△CPD中，

∠B=∠D ∠BPA=∠DPC AP=CP

，
∴△APB≌△CPD（AAS）；
④在△APB和△CPD中，

∠BPA=∠DPC BP=CP ∠A=∠C

，
∴△APB≌△CPD（ASA），
则②③④均可作为判定△APB≌△CPD的论断，只有①不能作为判定△APB≌△CPD的论断．
故答案为：①．

点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．