Question

【题目】在四边形中，，，是对角线，于点，于点

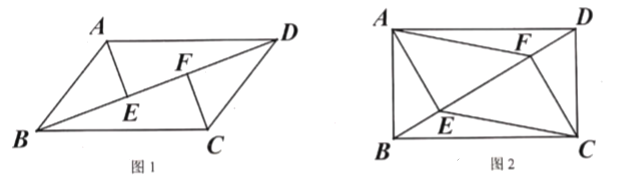
(1)如图1，求证：

(2)如图2，当时，连接、，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形，使写出的每个三角形的面积都等于四边形面积的．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）根据平行线的性质可得，然后根据AAS即可证得结论；

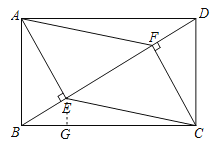
（2）由已知条件、直角三角形的性质和平行线的性质可依次得出∠BAE=30°，∠ABE＝60°，∠ADB＝30°，然后利用30°角的直角三角形的性质可得BE与AB，AE与AD的关系，进而可得△ABE的面积=四边形ABCD的面积，即得△CDF的面积与四边形ABCD的面积的关系；作EG⊥BC于G，由直角三角形的性质得出EG与AB的关系，进而可得△BCE的面积＝四边形ABCD的面积，同理可得△ADF的面积与四边形ABCD的面积的关系，问题即得解决．

（1）证明：，，

，，

，

≌（AAS），

；

（2）△ABE的面积＝△CDF的面积＝△BCE的面积＝△ADF的面积＝四边形ABCD面积的．理由如下：

∵AD=BC，，DB=BD，∴△ADB≌△CBD，∴四边形ABCD的面积=2×△ABD的面积= AB×AD，

∵，∴∠BAE=30°，

∴∠ABE＝60°，∠ADB＝30°，

∴BE＝AB，AE＝AD，

∴△ABE的面积＝BE×AE＝×AB×AD＝AB×AD＝四边形ABCD的面积；

∵△ABE≌△CDF，∴△CDF的面积═四边形ABCD的面积；

作EG⊥BC于G，如图所示：∵∠CBD＝∠ADB＝30°，∴EG＝BE＝×AB＝AB，

∴△BCE的面积＝BC×EG＝BC×AB＝BC×AB＝四边形ABCD的面积，

同理：△ADF的面积＝矩形ABCD的面积．