题目内容
(1)计算:
(-
-4
)-(3
-2
)
(2)解方程:
①(x-5)2=2(x-5)
②x2-4x-2=0.
(-
| 12 |
|
|
|
(2)解方程:
①(x-5)2=2(x-5)
②x2-4x-2=0.
考点:解一元二次方程-因式分解法,二次根式的加减法,解一元二次方程-配方法
专题:计算题
分析:(1)将括号中每一项化为最简二次根式,去括号合并同类二次根式后即可得到结果;
(2)①方程右边整体移项到左边,提前公因数x-5,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;②将方程常数项移到方程右边,方程左右两边都加上4,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
(2)①方程右边整体移项到左边,提前公因数x-5,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;②将方程常数项移到方程右边,方程左右两边都加上4,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
解答:解:(1)原式=(-2
-4×
)-(3×
-2×
)
=(-2
-
)-(
-
)
=-2
-
-
+
=-3
;
(2)①(x-5)2=2(x-5),
移项得:(x-5)2-2(x-5)=0,
分解因式得:(x-5)(x-7)=0,
可得:x-5=0或x-7=0,
解得:x1=5 x2=7;
②x2-4x-2=0,
变形得:x2-4x=2,
配方得:x2-4x+4=6,即(x-2)2=6,
开方得:x-2=±
,
解得:x1=2+
,x2=2-
.
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 2 |
=(-2
| 3 |
| 2 |
| 3 |
| 2 |
=-2
| 3 |
| 2 |
| 3 |
| 2 |
=-3
| 3 |
(2)①(x-5)2=2(x-5),
移项得:(x-5)2-2(x-5)=0,
分解因式得:(x-5)(x-7)=0,
可得:x-5=0或x-7=0,
解得:x1=5 x2=7;
②x2-4x-2=0,
变形得:x2-4x=2,
配方得:x2-4x+4=6,即(x-2)2=6,
开方得:x-2=±
| 6 |
解得:x1=2+
| 6 |
| 6 |
点评:此题考查了解一元二次方程-因式分解法,利用此方法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
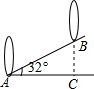 如图,坡角为32°的斜坡上两树间的水平距离AC为2米,则两树间的坡面距离AB为( )米.
如图,坡角为32°的斜坡上两树间的水平距离AC为2米,则两树间的坡面距离AB为( )米.| A、2cos32° | ||
| B、2tan32° | ||
| C、2sin32° | ||
D、
|
甲、乙两人从同一地点出发,沿同一方向跑步,速度分别为4米/秒和6米/秒,开始时甲先跑100米后乙再追赶,则从乙出发开始追上甲这一过程中,甲、乙两人之间的距离s(米)与甲跑步所用时间t(秒)之间的函数关系式为( )
| A、S=-10t+100(0≤t≤10) |
| B、S=-2t+100(0≤t≤50) |
| C、S=-2t+150(25≤t≤75) |
| D、S=2t-150(0≤t≤75) |
 如图所示,一个正方体和一个圆柱体紧靠在一起,则它们的主视图是( )
如图所示,一个正方体和一个圆柱体紧靠在一起,则它们的主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在⊙O中,AB为直径,AD为弦,过D点的直线与AB的延长线交于点C.
如图,在⊙O中,AB为直径,AD为弦,过D点的直线与AB的延长线交于点C. 如图所示,一朵三叶花由六段近似圆弧组成,每一段圆弧都是四分之一圆周,每个叶片两端间的弦长为2,则此三叶花的面积约为
如图所示,一朵三叶花由六段近似圆弧组成,每一段圆弧都是四分之一圆周,每个叶片两端间的弦长为2,则此三叶花的面积约为