题目内容
2.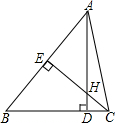 如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.
如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.
分析 根据直角三角形两锐角互余求出∠BAD,再根据∠CAD=∠BAC-∠BAD代入数据计算即可得解;然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠DHE=∠BAD+∠AEH计算即可得解.
解答 解:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=90°-48°=42°;
∵CE⊥AB,
∴∠AEC=90°,
由三角形的外角性质得,∠DHE=∠BAD+∠AEH=42°+90°=132°.
点评 本题考查了直角三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
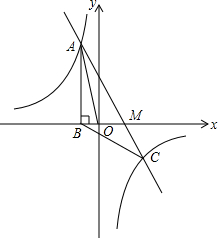 如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(-1,4),C(m,-2),AB⊥x轴,垂足为点B.
如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(-1,4),C(m,-2),AB⊥x轴,垂足为点B.