题目内容
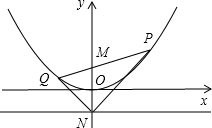
已知点A(a,b)为双曲线![]() (x>0)图象上一点.
(x>0)图象上一点.
(1)如图1所示,过点A作AD⊥y轴于D点,点P是x轴任意一点,连接AP.求△APD的面积.
(2)以A(a,b)为直角顶点作等腰Rt△ABC,如图2所示,其中点B在点C的左侧,若B点的坐标为B(﹣1,0),且a、b都为整数时,试求线段BC的长.
(3)在(2)中,当等腰Rt△ABC的直角顶点A(a,b)在双曲线上移动时,B、C两点也随着移动,试用含a,b的式子表示C点坐标;并证明在移动过程中OC2﹣OB2的值恒为定值.

考点:
反比例函数综合题..
分析:
(1)由点A(a,b)在反比例函数![]() 上可得到ab=6,AD=a,OD=b,进而根据三角形的面积公式求出△APD的面积;
上可得到ab=6,AD=a,OD=b,进而根据三角形的面积公式求出△APD的面积;
(2)过A作AE垂直x轴于E点,可得:E(a,0),由∠ABE=45°可得△ABE为等腰直角三角形,根据AE=BE,求出a和b的值,进而求出BC的长;
(3)分类讨论B点在y轴的左侧还是在y轴的右侧,求出C点的坐标,可得OC的长,再用a和b表示出OB的长,两式相减,观察得到的结果是否为定值.
解答:
解:(1)由点A(a,b)在反比例函数![]() 上可得:
上可得:
ab=6,AD=a,OD=b,
所以![]() ,
,
(2)过A作AE垂直x轴于E点,可得:E(a,0),
则由∠ABE=45°可得△ABE为等腰直角三角形,
∴AE=BE,
E在B右侧且B坐标为(﹣1,0),
∴BE=a﹣(﹣1)=a+1,则a+1=b,
又∵ab=6且a、b都为整数.
∴a只能取2,b为3,
此时,BE=AE=CE=b=3,
∴BC=BE+CE=6,
(3)由(2)可知:EC=AE=BE=b;且不管点A如何移动,总有:OC=OE+EC=a+b,且C总在x轴正半轴,
∴C(a+b,0),
当B在y轴左侧时,如图2所示,则a<b,
OB=BE﹣OE=b﹣a.
(a+b)2﹣(b﹣a)2=a2+2ab+b2﹣a2+2ab﹣b2=4ab=4×6=24,
∴OC2﹣OB2=24,
当B在y轴右侧或与原点重合时,
如图4所示,则a≥b,
∴OB=OE﹣BE=a﹣b,
∴OC2﹣OB2=(a+b)2﹣(a﹣b)2=a2+2ab+b2﹣a2+2ab﹣b2=4ab=4×6=24综上所述:移动过程中OC2﹣OB2的值恒为24.


点评:
本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握反比例函数的性质以及等腰三角形等知识,此题考查了分类讨论的解题思路,此题难度有点大.

 发沿线路DC?CB?BA做匀速运动.
发沿线路DC?CB?BA做匀速运动.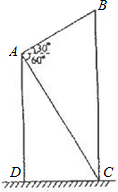 在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为15cm.求旗杆的高度.
在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为15cm.求旗杆的高度.