题目内容
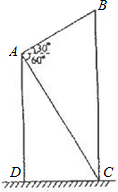在一次数学课外活动中，一位同学在教学楼的点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为15cm．求旗杆的高度．
分析：过A作AE⊥BC，构造两个直角三角形，然后利用解直角三角形的知识解答．
解答：
解：过A作AE⊥BC，垂足为E，由题意可知，四边形ADCE为矩形，
∴EC=AD=15，
在Rt△AEC中，tan∠EAC=
，
∴AE=
=
=5
（cm），
在Rt△AEB中，tan∠BAE=
，
∴BE=AE•tan∠EAB=5
•tan30°=5（cm），
∴BC=CE+BE=20（cm）．
答：旗杆高度为20厘米．
解：过A作AE⊥BC，垂足为E，由题意可知，四边形ADCE为矩形，∴EC=AD=15，
在Rt△AEC中，tan∠EAC=
| CE |
| AE |
∴AE=
| CE |
| tan∠EAC |
| 15 |
| tan60° |
| 3 |
在Rt△AEB中，tan∠BAE=
| BE |
| AE |
∴BE=AE•tan∠EAB=5
| 3 |
∴BC=CE+BE=20（cm）．
答：旗杆高度为20厘米．
点评：此题考查了解直角三角形的知识，作出辅助线，构造直角三角形是解题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
如图，在一次数学课外活动中，测得电线杆底部B与钢缆固定点C的距离为4米，钢缆与地面的夹角为60度，则这条钢缆在电线杆上的固定点A到地面的距离AB是
如图，在一次数学课外活动中，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向，办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离（结果精确到0.1米）．（供选用的数据：
≈1.414，
≈1.732）．
≈1.414，
≈1.732）．