题目内容
1．
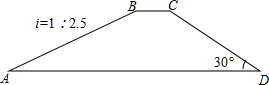如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30°，则坝底AD=56+20$\sqrt{3}$．
分析 过梯形上底的两个顶点向下底引垂线，得到两个直角三角形和一个矩形，利用相应的性质求解即可．
解答 解：作BE⊥AD，CF⊥AD，垂足分别为点E，F，则四边形BCFE是矩形，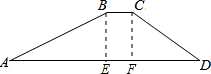
由题意得，BC=EF=6米，BE=CF=20米，斜坡AB的坡度i为1：2.5，
在Rt△ABE中，
∵$\frac{BE}{AE}$=$\frac{1}{2.5}$，
∴AE=50米，
在Rt△CFD中，
∵∠D=30°，
∴DF=CFcot∠D=20$\sqrt{3}$米，
∴AD=AE+EF+FD=50+6+20$\sqrt{3}$=（56+20$\sqrt{3}$）米．
故答案为：56+20$\sqrt{3}$．
点评 本题考查了坡度及坡角的知识，解答本题的关键是构造直角三角形和矩形，注意理解坡度与坡角的定义．
练习册系列答案
相关题目
11．在平面直角坐标系中，点P在第四象限，且点P到x轴的距离是3，到y轴的距离是2，则点P的坐标为（ ）
| A． | （-2，3） | B． | （-3，2） | C． | （3，2） | D． | （2，-3） |
如图，在平行四边形ABCD中，如果AE∥CF，那么BE与DF有怎样的数量关系？请说明理由．
9．已知点M（2m-1，3m+5）到y轴的距离是它到x轴距离的2倍，则m的值为（ ）
| A． | -$\frac{11}{4}$ | B． | 7 | C． | 7或-$\frac{3}{7}$ | D． | -$\frac{11}{4}$或-$\frac{9}{8}$ |
．