题目内容
当b≠0时,我们称直线y=bx+k为直线y=kx+b(k≠0)的伴随直线,现直线y=kx+b(k>b>0)与x轴、y轴的交点分别为A、B,它的伴随直线与x轴、y轴的交点分别为C、D,如果△AOD和△COB相似,则kb的值为
- A.2
- B.-2
- C.1
- D.-1
C
分析:先求出直点A、B、C、D的坐标分别是(- ,0)(0,b)(-
,0)(0,b)(- ,0)(0,k),再得出OA=
,0)(0,k),再得出OA= ,OC=
,OC= ,OB=b,OD=k,最后分当△AOD∽△COB和△AOD∽△BOC时两种情况分别得出
,OB=b,OD=k,最后分当△AOD∽△COB和△AOD∽△BOC时两种情况分别得出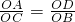 ,
,
 ,再把OA=
,再把OA= ,OC=
,OC= ,OB=b,OD=k代入即可求出kb的值.
,OB=b,OD=k代入即可求出kb的值.
解答: 解:∵直线y=kx+b(k>b>0)与x轴、y轴的交点分别为A、B,它的伴随直线与x轴、y轴的交点分别为C、D,
解:∵直线y=kx+b(k>b>0)与x轴、y轴的交点分别为A、B,它的伴随直线与x轴、y轴的交点分别为C、D,
∴点A、B、C、D的坐标分别是(- ,0)(0,b)(-
,0)(0,b)(- ,0)(0,k),
,0)(0,k),
∴OA= ,OC=
,OC= ,OB=b,OD=k,
,OB=b,OD=k,
当△AOD∽△COB时,
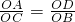 ,
,
 =
= ,
,
解得k=b(舍去),
当△AOD∽△BOC时
 ,
,
 ,
,
bk= =1,
=1,
故选:C.
点评:此题考查了一次函数综合,关键是根据函数图象求出交点坐标及线段长度,再根据相似三角形的性质列出式子,解题时要注意分两种情况讨论.
分析:先求出直点A、B、C、D的坐标分别是(-
 ,0)(0,b)(-
,0)(0,b)(- ,0)(0,k),再得出OA=
,0)(0,k),再得出OA= ,OC=
,OC= ,OB=b,OD=k,最后分当△AOD∽△COB和△AOD∽△BOC时两种情况分别得出
,OB=b,OD=k,最后分当△AOD∽△COB和△AOD∽△BOC时两种情况分别得出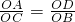 ,
, ,再把OA=
,再把OA= ,OC=
,OC= ,OB=b,OD=k代入即可求出kb的值.
,OB=b,OD=k代入即可求出kb的值.解答:
 解:∵直线y=kx+b(k>b>0)与x轴、y轴的交点分别为A、B,它的伴随直线与x轴、y轴的交点分别为C、D,
解:∵直线y=kx+b(k>b>0)与x轴、y轴的交点分别为A、B,它的伴随直线与x轴、y轴的交点分别为C、D,∴点A、B、C、D的坐标分别是(-
 ,0)(0,b)(-
,0)(0,b)(- ,0)(0,k),
,0)(0,k),∴OA=
 ,OC=
,OC= ,OB=b,OD=k,
,OB=b,OD=k,当△AOD∽△COB时,
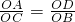 ,
, =
= ,
,解得k=b(舍去),
当△AOD∽△BOC时
 ,
, ,
,bk=
 =1,
=1,故选:C.
点评:此题考查了一次函数综合,关键是根据函数图象求出交点坐标及线段长度,再根据相似三角形的性质列出式子,解题时要注意分两种情况讨论.

练习册系列答案
相关题目