题目内容
9.已知a+b=2,求$\frac{1}{4}$a2+$\frac{1}{2}$ab+$\frac{1}{4}$b2的值.分析 先提公因式$\frac{1}{4}$,再用完全平方公式将$\frac{1}{4}$a2+$\frac{1}{2}$ab+$\frac{1}{4}$b2变形为$\frac{1}{4}$(a+b)2,然后将a+b=2代入计算即可.
解答 解:$\frac{1}{4}$a2+$\frac{1}{2}$ab+$\frac{1}{4}$b2=$\frac{1}{4}$(a2+2ab+b2)=$\frac{1}{4}$(a+b)2,
当a+b=2时,
原式=$\frac{1}{4}$×22=$\frac{1}{4}$×4=1.
点评 本题考查了因式分解的应用以及代数式求值,能够将$\frac{1}{4}$a2+$\frac{1}{2}$ab+$\frac{1}{4}$b2因式分解为$\frac{1}{4}$(a+b)2,是解题的关键.

练习册系列答案
相关题目
17. 西山隧道段是上庄路南延工程的一部分,将穿越西山山脉,隧道全长约4km.隧道贯通后,往来海淀山前山后地区较之前路程有望缩短一半,其主要依据是( )
西山隧道段是上庄路南延工程的一部分,将穿越西山山脉,隧道全长约4km.隧道贯通后,往来海淀山前山后地区较之前路程有望缩短一半,其主要依据是( )
 西山隧道段是上庄路南延工程的一部分,将穿越西山山脉,隧道全长约4km.隧道贯通后,往来海淀山前山后地区较之前路程有望缩短一半,其主要依据是( )
西山隧道段是上庄路南延工程的一部分,将穿越西山山脉,隧道全长约4km.隧道贯通后,往来海淀山前山后地区较之前路程有望缩短一半,其主要依据是( )| A. | 两点确定一条直线 | B. | 两点之间,线段最短 | ||
| C. | 直线比曲线短 | D. | 两条直线相交于一点 |
1.三种图书的单价分别为10元、15元和20元,某学校计划恰好用500元购买上述图书30本,那么不同的购书方案有( )
| A. | 9种 | B. | 10种 | C. | 11种 | D. | 12种 |
 如图,以O为位似中心,在网格内作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.
如图,以O为位似中心,在网格内作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.
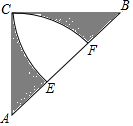 如图,等腰直角三角形ABC中,∠C=90°,∠A=45°,直角边AC=BC=a,分别以点A点B为圆心以直角边为半径作弧交AB于点E,F.
如图,等腰直角三角形ABC中,∠C=90°,∠A=45°,直角边AC=BC=a,分别以点A点B为圆心以直角边为半径作弧交AB于点E,F.