Question

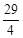 （2013年四川南充3分） 如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm，已知y与t的函数关系的图形如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；②当0＜t≤5时，；③直线NH的解析式为；④若△ABE与△QBP相似，则t=秒。其中正确的结论个数为【    】

A. 4             B. 3                C. 2                                                D. 1

 

Answer 1

【答案】

B。

【解析】根据图（2）可得，当点P到达点E时点Q到达点C，

 ∵点P、Q的运动的速度都是1cm/秒，

∴BC=BE=5cm。∴AD=BE=5，故结论①正确。

如图1，过点P作PF⊥BC于点F，

根据面积不变时△BPQ的面积为10，可得AB=4，

∵AD∥BC，∴∠AEB=∠PBF。

∴。

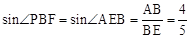∴PF=PBsin∠PBF=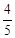t。

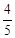∴当0＜t≤5时，y=BQ•PF=t•t=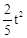。故结论②正确。

根据5～7秒面积不变，可得ED=2，

当点P运动到点C时，面积变为0，此时点P走过的路程为BE+ED+DC=11，故点H的坐标为（11，0）。

设直线NH的解析式为y=kx+b，

将点H（11，0），点N（7，10）代入可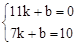得：，解得：。

∴直线NH的解析式为：。故结论③错误。

如图2，当△ABE与△QBP相似时，点P在DC上，

∵tan∠PBQ=tan∠ABE=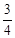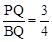，∴，即。

解得：t=。故结论④正确。

综上所述，①②④正确，共3个。故选B。

考点：动点问题的函数图象，双动点问题，矩形的性质，锐角三角函数定义，待定系数法的应用，曲线上点的坐标与方程的关系，相似三角形的性质，分类思想的应用。