Question

（2013年四川南充8分）如图，二次函数y=x²+bx－3b+3的图象与x轴交于A、B两点（点A在点B的左边），交y轴于点C，且经过点（b－2，2b²－5b－1）.

（1）求这条抛物线的解析式；

（2）⊙M过A、B、C三点，交y轴于另一点D，求点M的坐标；

（3）连接AM、DM，将∠AMD绕点M顺时针旋转，两边MA、MD与x轴、y轴分别交于点E、F，若△DMF为等腰三角形，求点E的坐标.

 

Answer 1

【答案】

解：（1）把点（b－2，2b²－5b－1）代入y=x²+bx－3b+3，得

2b²－5b－1=（b－2）²+b（b－2）－3b+3， 解得b=2。

∴抛物线的解析式为y=x²+2x－3。

（2）由x²+2x－3=0，得x=－3或x=1。∴A（－3，0）、B（1，0）。

由x=0得y=－3，∴（0，－3）。

∵抛物线的对称轴是直线x=－1，圆心M在直线x=－1上，

∴设M（－1，n），作MG⊥x轴于G，MH⊥y轴于H，连接MC、MB。

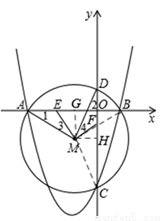
∴MH=1，BG=2。

∵MB=MC，∴BG²+MG²=MH²+CH²，

即4+n²=1+（3+n）²，解得n=－1。∴点M（－1，－1）。

（3）如图，由M（－1，－1），得MG=MH。

∵MA=MD，∴Rt△AMG≌RtDMH。∴∠1=∠2。

由旋转可知∠3=∠4， ∴△AME≌△DMF。

若△DMF为等腰三角形，则△AME为等腰三角形。  

设E（x，0），△AME为等腰三角形，分三种情况：

①AE=AM=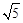，则x=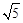－3，∴E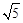（－3，0）。

②∵M在AB的垂直平分线上，∴MA=ME=MB，∴E（1，0）。      

③点E在AM的垂直平分线上，则AE=ME，

AE=x+3，ME²=MG²+EG²=1+（－1－x）²，

∴（x+3）²=1+（－1－x）²，解得x=，∴E（，0）。

∴所求点E的坐标为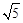（－3，0），（1，0），（，0）。

【解析】（1）将点（b－2，2b²－5b－1）代入抛物线解析式，求出未知数，从而得到抛物线的解析式。

（2）利用垂径定理及勾股定理，求出点M的坐标。

（3）首先，证明△AME≌△DMF，从而将“△DMF为等腰三角形”的问题，转化为“△AME为等腰三角形”的问题；其次，△AME为等腰三角形，可能有三种情形，需要分类讨论，逐一解析计算。

考点：二次函数综合题，旋转问题，曲线上点的坐标与方程的关系，垂径定理，勾股定理，全等三角形的判定和性质，等腰三角形的性质，分类思想的应用。