题目内容
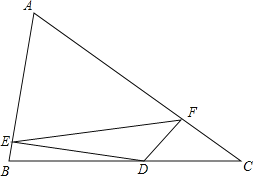
【题目】定义：在等腰三角形中，底边与腰的比叫做顶角的正对，顶角A的正对记作sadA，即sadA＝底边：腰．如图，在△ABC中，AB＝AC，∠A＝4∠B．则cosBsadA＝（ ）
A.1B.
C.
D.
【答案】B
【解析】
根据题意可以求得∠B的度数，然后根据锐角三角函数可以表示出AB和BC的值，从而可以求得sadA和cosA的值，进而求得cosBsadA的值．
∵在△ABC中，AB＝AC，∠A＝4∠B，
∴∠B＝∠C，
∵∠A+∠B+∠C＝180°，
∴6∠B＝180°，
解得，∠B＝30°，
作AD⊥BC于点D，设AD＝a，
则AB＝2a，BD＝
a，
∵BC＝2BD，
∴BC＝2a，
∴sadA＝
，cosB＝
，
∴cosBsadA＝
，
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
