Question

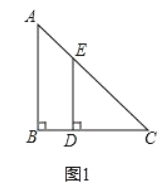
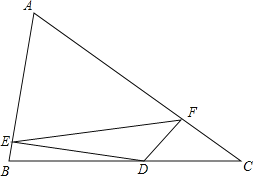
【题目】在△ABC中，AB＝5，AC＝8，BC＝7，点D是BC上一动点，DE⊥AB于E，DF⊥AC于F，线段EF的最小值为_____．

Answer 1

【答案】

【解析】

如图，作CM⊥AB于M，AN⊥BC于N．连接AD，OE，OF．设AM＝x，则BM＝5﹣x．根据，可得，解得x＝4，推出∠EAF＝60°，由A，E，D，F四点共圆，推出当⊙O的直径最小时，EF的长最小，根据垂线段最短可知：当AD与AN重合时，AD的值最小，由此即可解决问题．

解：如图，作CM⊥AB于M，AN⊥BC于N．连接AD，OE，OF．设AM＝x，则BM＝5﹣x．

∵CM2＝AC2﹣AM2＝BC2﹣BM2，

∴82﹣x2＝72﹣（5﹣x）2，

解得x＝4，

∴AM＝4，AC＝2AM，

∴∠ACM＝30°，∠CAM＝60°，CM＝AM＝4，

∵S△ABC＝BCAN＝ABCM，

∴AN＝，

∵DE⊥AB，DF⊥AC，

∴∠AED＝∠AFD＝90°，

∴A，E，D，F四点共圆，

∴当⊙O的直径最小时，EF的长最小，

根据垂线段最短可知：当AD与AN重合时，AD的值最小，AD的最小值为，

此时OE＝OF＝，EF＝2OEcos30°＝，

∴EF的最小值为，

故答案为.