��Ŀ����
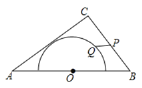
����Ŀ����ͼ����Rt��ABC�У���ACB��90����AC��6cm��BC��8cm����P�ӵ�A�������߶�AB��ÿ��1cm���ٶ��˶���ͬʱ��Q�ӵ�B����������B��C��A��ÿ��2cm���ٶ��˶�������һ��ֹͣ����һ��Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt�룮
��������ֱ��д��t��ȡֵ��Χ���� ����
�ڵ���P�˶���AB�е�ʱ������PQ��PC��BQ����֤����CPQ�ס�ABQ��
����������BPQ��ֱ��������ʱ����t��ֵ��
���𰸡���������0��t��7���ڼ�������������t��![]() ��
��![]()
��������
�����������ù��ɶ������AB�ij����ɽ�����⣮
���������Ƕ�Ӧ��������������Ƽ���֤����
���������������Σ�����ͼ2�У���PQ��ACʱ����PQB����C��90��������ͼ3�У�����QPB��90��ʱ���ֱ���⼴�ɣ�
���������⣺��Rt��ABC�У��ߡ�ACB��90����AC��6��BC��8��
��AB��![]() ��
��![]() ��10��
��10��
��![]() ��10��
��10��![]() ��7��7��10��
��7��7��10��
��t��ȡֵ��ΧΪ��![]() ��
��
�ʴ�Ϊ��0��t��7��
��֤������ͼ1�У��������P�˶���AB���е�ʱ��t��5��
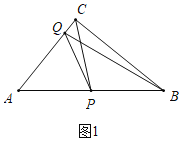
��CQ��5��2��8��2��
�ߡ�ACB��90����PA��PB��
��PC��PA��PB��5��
���PCQ����A��
��![]() ��
��![]() ��
��
��![]() ��
��
���QCP�ס�CAB��
�������⣺����ͼ2�У���PQ��ACʱ����PQB����C��90����
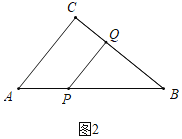
��PQ��AC��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
����ͼ3�У�����QPB��90��ʱ��
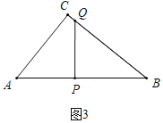
�ߡ�QPB����ACB��90������B����B��
���BPQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��������������������t��ֵΪ��![]() ��
��![]() .
.

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�