题目内容
 已知三个边长分别为10,6,4的正方形如图排列(点A,B,E,H在同一条直线上),DH交EF于R,则线段RN的值为( )
已知三个边长分别为10,6,4的正方形如图排列(点A,B,E,H在同一条直线上),DH交EF于R,则线段RN的值为( )| A、1 | B、2 | C、2.5 | D、3 |
分析:求RN的长,需先求出RE的值,易证得△HRE∽△HDA,根据得出的对应成比例线段即可求出RE的长,由此得解.
解答:解:∵RE∥AD,
∴△HRE∽△HDA;
∴
=
;
∵EH=4,AD=10,AH=AB+BE+EH=20,
∴RE=
=
=2;
∴RN=EN-ER=2;
故选B.
∴△HRE∽△HDA;
∴
| HE |
| HA |
| RE |
| AD |
∵EH=4,AD=10,AH=AB+BE+EH=20,
∴RE=
| HE•AD |
| HA |
| 4×10 |
| 20 |
∴RN=EN-ER=2;
故选B.
点评:此题主要考查的是正方形的性质以及相似三角形的判定和性质.

练习册系列答案
相关题目
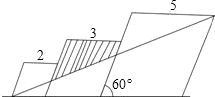 已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )
已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )| A、3.15 | B、3.75 | C、4 | D、4.35 |
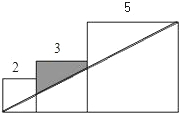 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为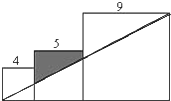 已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为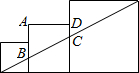 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是