题目内容
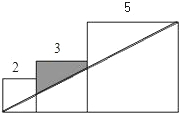 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为分析:根据△ABC∽△AMN,可将BC的长求出,由OB的长可将OC的长求出,同理根据△ABC∽△AEF,可将EF的长求出,由PE的长可将PF的长求出,代入梯形的面积公式可将阴影部分的面积求出.
解答: 解:∵BC∥MN
解:∵BC∥MN
∴
=
,即
=
,解得:BC=1
∵OB=3
∴OC=3-1=2
∵BC∥EF
∴
=
,即
=
,解得:EF=
∵PE=3
∴PF=3-
=
∴梯形OCFP的面积为:(2+
)×3×
=3.75
故图中阴影部分面积为3.75.
 解:∵BC∥MN
解:∵BC∥MN∴
| BC |
| MN |
| AB |
| AM |
| BC |
| 5 |
| 2 |
| 2+3+5 |
∵OB=3
∴OC=3-1=2
∵BC∥EF
∴
| BC |
| EF |
| AB |
| AE |
| 1 |
| EF |
| 2 |
| 2+3 |
| 5 |
| 2 |
∵PE=3
∴PF=3-
| 5 |
| 2 |
| 1 |
| 2 |
∴梯形OCFP的面积为:(2+
| 1 |
| 2 |
| 1 |
| 2 |
故图中阴影部分面积为3.75.
点评:利用三角形相似,可将阴影部分为梯形的上底和下底求出,进而可求出阴影部分的面积.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
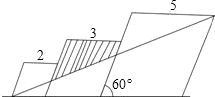 已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )
已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )| A、3.15 | B、3.75 | C、4 | D、4.35 |
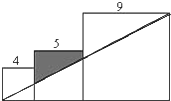 已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为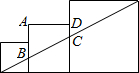 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是