题目内容
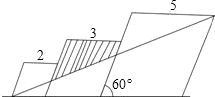 已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由菱形的性质来证明△ABH∽△ADE,再利用相似三角形对应边成比例的性质来求得BH的长;同理,求出CF的长度;然后根据三角形的边角关系求出菱形BCGJ的高;最后求出菱形BCGJ的面积和梯形BHFC的面积,进而求得阴影部分的面积.
解答: 解:
解:
在△ADE和△ABH中,∠HAB=∠EAD,
∵图中是三个菱形排列,
∴HB∥FC∥ED,
∴∠AHB=∠AED,∠ABH=∠ADE,
∴△ABH∽△ADE,
∴AB:AD=BH:DE;
又∵AB=2,AD=2+3+5=10,DE=5,
∴BH=1;
同理,求得CF=
;
∵菱形的较小锐角为60°,即∠HBC=∠FCD=60°,

∴梯形BHFC,即菱形JBCG的高JM=3×sin60°=
;
∴S梯形BHCF=
×(1+
)×
=
,
S菱形JBCG=3×
=
,
∴S阴影=S菱形JBCG-S梯形BHCF=
.
故选C.
 解:
解:在△ADE和△ABH中,∠HAB=∠EAD,
∵图中是三个菱形排列,
∴HB∥FC∥ED,
∴∠AHB=∠AED,∠ABH=∠ADE,
∴△ABH∽△ADE,
∴AB:AD=BH:DE;
又∵AB=2,AD=2+3+5=10,DE=5,
∴BH=1;
同理,求得CF=
| 5 |
| 2 |
∵菱形的较小锐角为60°,即∠HBC=∠FCD=60°,

∴梯形BHFC,即菱形JBCG的高JM=3×sin60°=
3
| ||
| 2 |
∴S梯形BHCF=
| 1 |
| 2 |
| 5 |
| 2 |
3
| ||
| 2 |
21
| ||
| 8 |
S菱形JBCG=3×
3
| ||
| 2 |
9
| ||
| 2 |
∴S阴影=S菱形JBCG-S梯形BHCF=
15
| ||
| 8 |
故选C.
点评:本题主要考查了相似三角形的判定与性质,梯形与菱形的面积以及三角形中的边角关系,是基础性比较强的一道题.

练习册系列答案
相关题目
 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )
已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )| A、3.15 | B、3.75 | C、4 | D、4.35 |
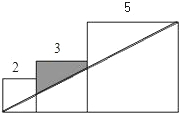 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为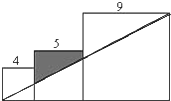 已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为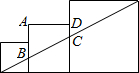 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是