题目内容
13.函数y=$\frac{\sqrt{x+4}}{x-2}$中自变量x的取值范围是x≥-4且x≠2.分析 根据二次根式的性质和分式的意义,被开方数大于等于0,可知:x+4≥0,分母不等于0,可知:x≠2,就可以求出自变量x的取值范围.
解答 解:根据题意得:$\left\{\begin{array}{l}{x+4≥0}\\{x-2≠0}\end{array}\right.$,
解得x≥-4且x≠2,
故答案为x≥-4且x≠2.
点评 本题考查使得分式和根号有意义的知识.函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
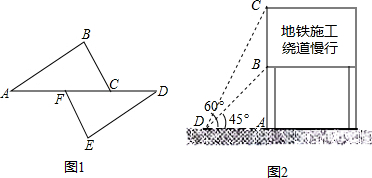
 如图,在?ABCD中,F是BC上的点,直线DF与AB的延长线相交于点E,与AC相交于点M,BP∥DF,且与AD相交于点P,与AC相交于点N,则图中的相似三角形有16对.
如图,在?ABCD中,F是BC上的点,直线DF与AB的延长线相交于点E,与AC相交于点M,BP∥DF,且与AD相交于点P,与AC相交于点N,则图中的相似三角形有16对.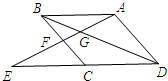 如图,已知E为?ABCD的边DC延长线上的一点,且CE=CD,联结AE分别交BC、BD于点F、G.那么$\frac{DG}{BD}$=$\frac{2}{3}$.
如图,已知E为?ABCD的边DC延长线上的一点,且CE=CD,联结AE分别交BC、BD于点F、G.那么$\frac{DG}{BD}$=$\frac{2}{3}$.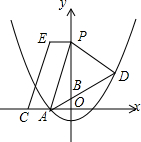 在平面直角坐标系中,A(-2,0),B(0,1),C(-4,0).点D(4,m)在直线AB上,抛物线y=$\frac{1}{4}$x2+bx+c恰好过A、D两点,点P(0,n)是抛物线对称轴上的一动点,将点P向左平移2个单位长度,对应点为E,连接PF、CE.
在平面直角坐标系中,A(-2,0),B(0,1),C(-4,0).点D(4,m)在直线AB上,抛物线y=$\frac{1}{4}$x2+bx+c恰好过A、D两点,点P(0,n)是抛物线对称轴上的一动点,将点P向左平移2个单位长度,对应点为E,连接PF、CE.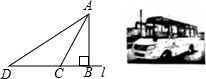 如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.
如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.