Question

13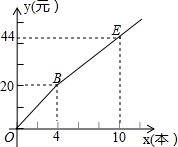． 如图，小明购买一种笔记本所付款金额y（元）与购买量x（本）之间的函数图象由线段OB和射线BE组成，则一次购买8个笔记本比分8次购买每次购买1个可节省4元．

Answer 1

分析 根据函数图象，分别求出线段OB和射线BE的函数解析式，然后可求出一次购买8个笔记本的价钱和分8次购买每次购买1个的花费，进而可得答案．

解答 解：由线段OB的图象可知，当0＜x＜4时，y=5x，
1个笔记本的价钱为：y=5，
设射线BE的解析式为y=kx+b（x≥4），
把（4，20），（10，44）代入得$\left\{\begin{array}{l}{20=4k+b}\\{44=10k+b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=4}\\{b=4}\end{array}\right.$，
∴射线BE的解析式为y=4x+4，
当x=8时，y=4×8+4=36，
5×8-36=4（元），
故答案为：4．

点评 本题考查了一次函数的应用，解决本题的关键是掌握待定系数法求一次函数解析式．