题目内容
下表给出了代数式x2+bx+c与x的一些对应值：
| x | …… | -1 | 0 | 1 | 2 | 3 | 4 | …… |
| x2+bx+c | …… | 3 | -1 | 3 | …… |
（1）根据表格中的数据，确定b、c的值，并填齐表格空白处的对应值；
（2）设y=x2 + bx + c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连结PC，当△PEC的面积最大时，求P点的坐标.
解：（1）当x=0和x=4时，均有函数值y=3,
∴ 函数的对称轴为x=2
∴顶点坐标为（2，-1）
即对应关系满足y=（x-2）2-1,
∴ y=x2－4x＋3
∴当x=-1时，y=8;x=1时，y=0;x=3时，y=0
| x | …… | -1 | 0 | 1 | 2 | 3 | 4 | …… |
| x2+bx+c | …… | 8 | 3 | 0 | -1 | 0 | 3 | …… |
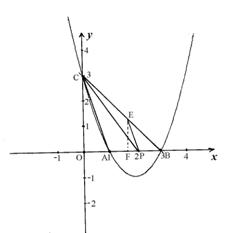（2） 解：函数图像与x轴交于A（1，0）、B（3，0）；
与y轴交于点C（0，3）
设P点坐标为（x,0），则PB=3－x
∴S△BCP=
(3－x)
∵PE∥AC
∴△BEP∽△BCA 作EF⊥OB于F
∴
=
即
=
∴ EF=(3－x)
∴S△BPE=
BP?EF=
（3-x）2
∵S△PEC= S△BCP－S△BPE
∴S△PEC =(3－x)－（3-x）2
S△PEC =－x2＋3x－
=－(x－2)2＋
∴当x=2时，y最大=
∴ P点坐标是（2，0）
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
（2）设y=x2+bx+c，则当x取何值时，y＞0；
（3）请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象？
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
（2）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 3 | -1 | 3 | … |
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |