题目内容
9.湖面上有一塔高15米,在塔顶A测得一气球的仰角为40°,又测得气球在水中像的俯角为60°,求气球高出水面的高度.(精确到0.1米)分析 根据题意,设气球的点为P点,作点P至湖面的对称点P′,连接PP′,与湖面的交点为O,连接AP′,OE为塔顶距离湖面的高度,结合直角三角形可得OP的大小,即得到答案.
解答 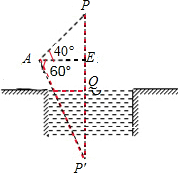 解:作点P至湖面的对称点P′,连接AP′,如图所示:
解:作点P至湖面的对称点P′,连接AP′,如图所示:
∵∠PAE=40°,∠EAP′=60°,
∴P′E=AEtan60°=$\sqrt{3}$AE.
设PE=x米,
∴PE=tan40°•x≈0.84x米,P′E=$\sqrt{3}$x≈1.73x米,
∴PP′=0.84x+1.73x=2.57x米.
∵物和像关于镜面对称,
∴PO=$\frac{1}{2}$PP′=1.285x米,
∴PE+OE=1.285x米,即0.84x+15=1,285x米,
解得x≈34.2,
∴PO≈43.9米.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用平面镜成像的特点和三角函数解直角三角形.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 3是9的算术平方根 | B. | -3是(-3)2的算术平方根 | ||
| C. | 0.64的立方根是0.4 | D. | $\sqrt{(-2)^{2}}$的平方根是±2 |
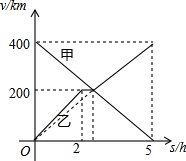 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.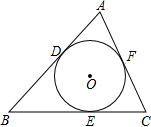 如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF.
如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF.