题目内容
1. 如图,已知EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.【解】∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补)
又∵∠BAC=60°(已知)
∴∠AGD=120°.
分析 根据平行线的性质得出∠2=∠3,求出∠1=∠3,根据平行线的判定得出AB∥DG,根据平行线的性质得出∠BAC+∠DGA=180°,代入求出即可.
解答 解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
又∵∠BAC=60°(已知),
∴∠AGD=120°,
故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠DGA,两直线平行,同旁内角互补,120°.
点评 本题考查了平行线的性质和判定,能灵活运用性质和判定定理进行推理是解此题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
11.计算正确的是( )
| A. | 3.4×104=340000 | B. | m×2m2=3m2 | C. | (-$\frac{1}{2}$mn2)2=m2n4 | D. | 4xy-4yx=0 |
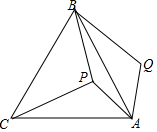 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
 用4根木棍可拼成大写的英文字母“M”,平移其中一根木棍,你能得到另一个大写的英文字母,请写出这个英文字母W.
用4根木棍可拼成大写的英文字母“M”,平移其中一根木棍,你能得到另一个大写的英文字母,请写出这个英文字母W.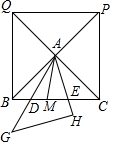 如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.
如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.