Question

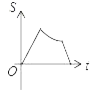
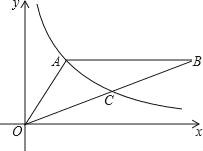
【题目】如图，双曲线y＝（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），则△OAB的面积_____．

Answer 1

【答案】9

【解析】

根据反比例函数y＝（x＞0）的图象经过△OAB的顶点A，点A的坐标为（2，3），可以求得k的值；再根据AB∥x轴，可知点A、B的纵坐标相等和OB的中点C，可得点C的纵坐标，由点C在反比例函数的图象上，可得点C的坐标，从而得到点B的坐标，从而可以求得△OAB的面积．

解：∵反比例函数y＝（x＞0）的图象经过△OAB的顶点A，点A的坐标为（2，3），

∴3＝，即k的值是6；

∵反比例函数y＝（x＞0）的图象经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），

∴点B的纵坐标是3，

∴点C的纵坐标是，

∴，

解得x＝4，

即点C的坐标是（4，），

∴点B的坐标是（8，3），

∴△OAB的面积是×3×（8﹣2）＝9，

故答案为：9．