题目内容
23、某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.

(1)现有正方形纸板162张,长方形纸板若干张.若要做两种纸盒共100个,设做竖式纸盒x个.①根据题意,完成以下表格;

②求出当恰好用完正方形纸板时两种纸盒各做多少个.
③此对长方形纸板用
(2)若每张正方形纸板成本为2元,每张长方形纸板成本为3元,现要做两种纸盒共108个,且两种纸盒成本一样多,则竖式纸盒做

(1)现有正方形纸板162张,长方形纸板若干张.若要做两种纸盒共100个,设做竖式纸盒x个.①根据题意,完成以下表格;

②求出当恰好用完正方形纸板时两种纸盒各做多少个.
③此对长方形纸板用
338
张.(2)若每张正方形纸板成本为2元,每张长方形纸板成本为3元,现要做两种纸盒共108个,且两种纸盒成本一样多,则竖式纸盒做
52
个.(已知两种纸板有足够多)分析:(1)可根据竖式纸盒+横式纸盒=100个,每个竖式纸盒需1个正方形纸板和4个长方形纸板,每个横式纸盒需3个长方形纸板和2个正方形纸板来填空.
(2)设出竖式纸盒的数量,然后根据(1)及两种纸盒成本一样多可得出方程,解出即可.
(2)设出竖式纸盒的数量,然后根据(1)及两种纸盒成本一样多可得出方程,解出即可.
解答:解:①由题意可补充图表得:

②恰好用完正方形纸板时两种纸盒时,x+2(100-x)=162,
解得:x=38,
由x=38得,100-38=62,
答:此时竖式纸盒做38个,横式纸盒做62个.
③长方形纸板用了38×4+62×3=338个;
(2)设竖式纸盒做了x个,横式做了108-x个,
由题意得:4×3x+2x=3×3(108-x)+2×2(108-x),
解得:x=52.
即竖式纸盒做了52个.

②恰好用完正方形纸板时两种纸盒时,x+2(100-x)=162,
解得:x=38,
由x=38得,100-38=62,
答:此时竖式纸盒做38个,横式纸盒做62个.
③长方形纸板用了38×4+62×3=338个;
(2)设竖式纸盒做了x个,横式做了108-x个,
由题意得:4×3x+2x=3×3(108-x)+2×2(108-x),
解得:x=52.
即竖式纸盒做了52个.
点评:本题考查一元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题根据竖式及横式的组成得出方程求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)
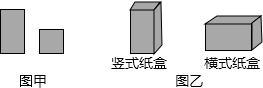
(1)现有正方形纸板50张,长方形纸板100张,若要做竖式纸盒个x,横式纸盒y个.
①根据题意,完成以下表格:
②若纸板全部用完,求x、y的值;
(2)若有正方形纸板90张,长方形纸板a张(a是整数),做成上述两种纸盒,纸板恰好全部用完.已知164<a<174,求a的值.

(1)现有正方形纸板50张,长方形纸板100张,若要做竖式纸盒个x,横式纸盒y个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | |
| 长方形纸板(张) | 3y |
(2)若有正方形纸板90张,长方形纸板a张(a是整数),做成上述两种纸盒,纸板恰好全部用完.已知164<a<174,求a的值.
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒 .
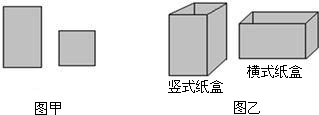
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.

(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
纸盒 纸板 |
竖式纸盒(个) | 横式纸盒(个) |
| x | 100-x | |
| 正方形纸板(张) | 2(100-x) | |
| 长方形纸板(张) | 4x |
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.
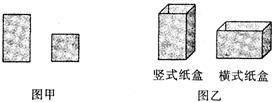 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)(1)现有正方形纸板50张,长方形纸板l 00张,若要做竖式纸盒x个,横式纸盒y个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | |
| 长方形纸板(张) | 3y |
(2)若有正方形纸板80张,长方形纸板n张,做成上述两种纸盒,纸板恰好全部用完.已知162<n<172,求n的值.
 (2012•新疆)某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
(2012•新疆)某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?