题目内容
8.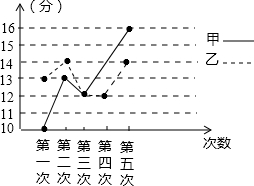 王老师为了从班级里数学比较优秀的甲、乙两位同学中选拔一人参加“全国初中数学希望杯竞赛”,对两位同学进行了5次测验,测验成绩情况如图表所示:.
王老师为了从班级里数学比较优秀的甲、乙两位同学中选拔一人参加“全国初中数学希望杯竞赛”,对两位同学进行了5次测验,测验成绩情况如图表所示:.请利用图表中提供的数据,解答下列问题:
(1)根据图中分别写出甲、乙五次的成绩:
甲:10,13,12,14,16;乙:13,14,12,12,14.
(2)填写完成下列表格:
| 平均成绩 | 中位数 | 众数 | 方差 | |
| 甲 | 13 | 13 | 无 | 4 |
| 乙 | 13 | 13 | 12和14 | 0.8 |
分析 (1)从折线统计图中读出两人的成绩;
(2)根据平均数的定义求甲的平均数;把乙的成绩按由小到大排列,然后根据中位数、众数的定义和方差公式求解;
(3)比较方差的大小,通过判断甲乙成绩的稳定性进行选择.
解答 解:(1)用折线统计图得甲的成绩为:10,13,12,14,16;乙的成绩为:13,14,12,12,14;
(2)甲的平均数=$\frac{1}{5}$(10+13+12+14+16)=13,
乙的成绩按由小到大排列为:12,12,13,14,14,
所以乙的中位数为13,众数为12和14,方差=$\frac{1}{5}$[(12-13)2+[(12-13)2+[(13-13)2+[(14-13)2+[(14-13)2]=0.8;
(3)选乙去竞赛.理由如下:
甲乙两人的平均数相同,中位数相等,但乙的成绩比较稳定,所以选乙去.
故答案为10,13,12,14,16;13,14,12,12,14;13,13,12和14,0.8.
点评 本题考查了折线统计图:折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.也考查了中位数、众数和方差.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18.已知等腰三角形的周长为20cm,底边长为ycm,腰长为xcm,则y与x之间的函数关系式为( )
| A. | y=20-2x(0<x<10) | B. | y=10-x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=10-x(5<x<10) |
19.对于多项式①x2-y2,②-x2-y2,③4x2-y,④x2-4,能够用平方差公式进行因式分解的是( )
| A. | ①和② | B. | ①和③ | C. | ①和④ | D. | ②和④ |
16.某校为了充实师资力量,决定招聘一位数学教师,对应聘者进行笔试和试讲两项综合考核,根据重要性,笔试成绩占30%,试讲成绩占70%,应聘者王晓、张会两人的得分如下表,如果你是校长,你会录用谁?请说明理由.
| 姓名 | 笔试 | 试讲 |
| 王晓 | 81分 | 95分 |
| 张会 | 90分 | 82分 |
3.关于x的不等式2x-10>-5的最小整数解为( )
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
20.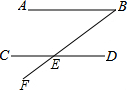 如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
 如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )| A. | 120° | B. | 60° | C. | 150° | D. | 30° |
17.已知:x+y=8,xy=12,则x2+y2的值是( )
| A. | 40 | B. | 48 | C. | 80 | D. | 88 |
18.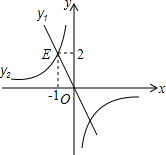 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )| A. | x<-1 | B. | -1<x<0 | C. | x>1 | D. | 0<x<1 |
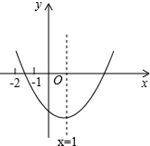 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac; ②abc>0; ③2a-b=0; ④8a+c<0; ⑤9a+3b+c<0. 其中结论正确的是①②⑤.(填正确结论的序号)(③根据对称轴判断,④根据韦达定理的两根积判断)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac; ②abc>0; ③2a-b=0; ④8a+c<0; ⑤9a+3b+c<0. 其中结论正确的是①②⑤.(填正确结论的序号)(③根据对称轴判断,④根据韦达定理的两根积判断)