题目内容
 正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,它们的面积分别为m,n(如图)则
正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,它们的面积分别为m,n(如图)则| m |
| n |
| 9 |
| 8 |
| 9 |
| 8 |
分析:由正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,易得△AGM、△AEP,△CFP,△CNH是等腰直角三角形,即可得GH=
AC,EP=
AC,继而求得答案.
| 1 |
| 3 |
| ||
| 4 |
解答: 解:如图,∵正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,
解:如图,∵正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,
∴∠DAG=45°,∠AGM=90°,
∴△AGM是等腰直角三角形,
同理可得:△AEP,△CFP,△CNH是等腰直角三角形,
∴AG=MG=NH=CH=GH=
AC,AE=EP=PF=CF,
∵AP=
EP,CP=
PF,
∴AP=PC=
AC,
∴EP=
AC,
∴m=EP2=
AC2,n=GH2=
AC2,
∴
=
.
故答案为:
.
 解:如图,∵正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,
解:如图,∵正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,∴∠DAG=45°,∠AGM=90°,
∴△AGM是等腰直角三角形,
同理可得:△AEP,△CFP,△CNH是等腰直角三角形,
∴AG=MG=NH=CH=GH=
| 1 |
| 3 |
∵AP=
| 2 |
| 2 |
∴AP=PC=
| 1 |
| 2 |
∴EP=
| ||
| 4 |
∴m=EP2=
| 1 |
| 8 |
| 1 |
| 9 |
∴
| m |
| n |
| 9 |
| 8 |
故答案为:
| 9 |
| 8 |
点评:此题考查了等腰直角三角形的性质以及正方形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒).
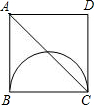
E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒). (2012•台湾)如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则小正方形的边长为何?( )
(2012•台湾)如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则小正方形的边长为何?( )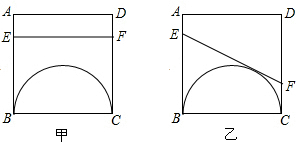 如图,正方形ABCD中,有一直径为BC的半圆,BC=2厘米,现有两点E、F,分别从点B,点A同时出发,点E沿线段BA以1厘米/秒的速度向点A运动,点F沿折线A-D-C以2厘米/秒的速度向C运动,设点E离开B的时间为t秒.
如图,正方形ABCD中,有一直径为BC的半圆,BC=2厘米,现有两点E、F,分别从点B,点A同时出发,点E沿线段BA以1厘米/秒的速度向点A运动,点F沿折线A-D-C以2厘米/秒的速度向C运动,设点E离开B的时间为t秒. 附加题:(成绩只作参考,不计入总分)
附加题:(成绩只作参考,不计入总分)