题目内容
(2011•鞍山)如图,在平面直角坐标系中,正方形ABCD的边长为
,点A在y轴正半轴上,点B在x轴负半轴上,B(-1,0),C、D两点在抛物线y=
x2+bx+c上.
(1)求此抛物线的表达式;
(2)正方形ABCD沿射线CB以每秒
个单位长度平移,1秒后停止,此时B点运动到B1点,试判断B1点是否在抛物线上,并说明理由;
(3)正方形ABCD沿射线BC平移,得到正方形A2B2C2D2,A2点在x轴正半轴上,求正方形AB CD的平移距离.
CD的平移距离.
| 5 |
| 1 |
| 2 |
(1)求此抛物线的表达式;
(2)正方形ABCD沿射线CB以每秒
| 5 |
(3)正方形ABCD沿射线BC平移,得到正方形A2B2C2D2,A2点在x轴正半轴上,求正方形AB
 CD的平移距离.
CD的平移距离.分析:(1)首先作出辅助线证明Rt△BCE≌Rt△ABO,进而得出CE=BO,BE=AO,同理可得△ADF≌△ABO,再求出C(1,-1)、D(2,1)即可求出抛物线解析式;
(2)根据题意,得1秒后点B移动的长度为,则 BB1=
,进而求出Rt△ABO≌Rt△BB1N,从而得出B1坐标,得出答案即可;
(3)首先证明△A2BB2∽△BAO,再求出正方形ABCD平移的距离.
(2)根据题意,得1秒后点B移动的长度为,则 BB1=
| 5 |
(3)首先证明△A2BB2∽△BAO,再求出正方形ABCD平移的距离.
解答: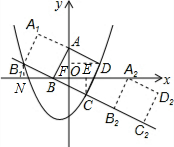 解:(1)如图,过点C作CE⊥x轴于点E,过点D作DF⊥y轴于点F.
解:(1)如图,过点C作CE⊥x轴于点E,过点D作DF⊥y轴于点F.
∵正方形ABCD中,AB=BC,∠ABC=∠AOB=90°,
即∠OBC+∠ABO=∠BAO+∠ABO=90°.
∴∠OBC=∠BAO.
在Rt△BCE和Rt△ABO中,
∵∠OBC=∠BAO,BC=AB,∠CEB=∠BOA=90°,
∴Rt△BCE≌Rt△ABO(AAS).
∴CE=BO,BE=AO.
∵B(-1,0),
∴BO=1.
∵AB=
,
∴在Rt△ABO中,由勾股定理,得AO=
=
=2.
∴CE=1,BE=2.
∴OE=BE-BO=1.
∴C(1,-1).
同理可得△ADF≌△ABO.
∴DF=AO=2,AF=BO=1.
∴OF=AO-AF=2-1=1.
∴D(2,1).
将C(1,-1)、D(2,1)分别代入y=
x2+bx+c中,
可得
解得
∴此抛物线的表达式为y=
x2+
x-2.
(2)点B1在抛物线上.
理由:根据题意,得1秒后点B移动的长度为,
×1=
,
则 BB1=
.
如图,过点B1作B1N⊥x轴于点N.
在Rt△ABO与Rt△BNB1中,
∵∠AOB=∠BNB1=90°,
∠2=∠B1BN=90°-∠ABO,AB=B1B,
∴Rt△ABO≌Rt△BB1N.
∴B1N=BO=1,NB=AO=2.
∴NO=NB+BO=2+1=3.
∴B1(-3,1).
将点B1(-3,1)代入y=
x2+
x-2中,可得点B1(-3,1)在抛物线上.
(3)如图,设正方形ABCD沿射线BC平移后的图形为正方形A2B2C2D2.
∵∠OBC=∠BAO,∠BB2A2=∠AOB,
∴△A2BB2∽△BAO.
∴
=
.
∵AO=2,BO=1,A2B2=
,
即
=
,
∴BB2=2
.
∴正方形ABCD平移的距离为2
.
 解:(1)如图,过点C作CE⊥x轴于点E,过点D作DF⊥y轴于点F.
解:(1)如图,过点C作CE⊥x轴于点E,过点D作DF⊥y轴于点F.∵正方形ABCD中,AB=BC,∠ABC=∠AOB=90°,
即∠OBC+∠ABO=∠BAO+∠ABO=90°.
∴∠OBC=∠BAO.
在Rt△BCE和Rt△ABO中,
∵∠OBC=∠BAO,BC=AB,∠CEB=∠BOA=90°,
∴Rt△BCE≌Rt△ABO(AAS).
∴CE=BO,BE=AO.
∵B(-1,0),
∴BO=1.
∵AB=
| 5 |
∴在Rt△ABO中,由勾股定理,得AO=
| AB2-BO2 |
| 5-1 |
∴CE=1,BE=2.
∴OE=BE-BO=1.
∴C(1,-1).
同理可得△ADF≌△ABO.
∴DF=AO=2,AF=BO=1.
∴OF=AO-AF=2-1=1.
∴D(2,1).
将C(1,-1)、D(2,1)分别代入y=
| 1 |
| 2 |
可得
|
解得
|
∴此抛物线的表达式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)点B1在抛物线上.
理由:根据题意,得1秒后点B移动的长度为,
| 5 |
| 5 |
则 BB1=
| 5 |
如图,过点B1作B1N⊥x轴于点N.
在Rt△ABO与Rt△BNB1中,
∵∠AOB=∠BNB1=90°,
∠2=∠B1BN=90°-∠ABO,AB=B1B,
∴Rt△ABO≌Rt△BB1N.
∴B1N=BO=1,NB=AO=2.
∴NO=NB+BO=2+1=3.
∴B1(-3,1).
将点B1(-3,1)代入y=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图,设正方形ABCD沿射线BC平移后的图形为正方形A2B2C2D2.
∵∠OBC=∠BAO,∠BB2A2=∠AOB,
∴△A2BB2∽△BAO.
∴
| BB2 |
| A2B2 |
| AO |
| BO |
∵AO=2,BO=1,A2B2=
| 5 |
即
| BB2 | ||
|
| 2 |
| 1 |
∴BB2=2
| 5 |
∴正方形ABCD平移的距离为2
| 5 |
点评:此题主要考查了二次函数的综合应用以及全等三角形的应用和相似三角形的应用,熟练利用判定得出点的坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为
(2011•鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为 (2011•鞍山)如图,矩形ABCD的对角线AC⊥OF,边CD在OE上,∠BAC=70°,则∠EOF等于( )
(2011•鞍山)如图,矩形ABCD的对角线AC⊥OF,边CD在OE上,∠BAC=70°,则∠EOF等于( ) (2011•鞍山)如图,?ABCD中,E、F分别为AD、BC上的点,且DE=2AE,BF=2FC,连接BE、AF交于点H,连接DF、CE交于点G,则
(2011•鞍山)如图,?ABCD中,E、F分别为AD、BC上的点,且DE=2AE,BF=2FC,连接BE、AF交于点H,连接DF、CE交于点G,则