题目内容
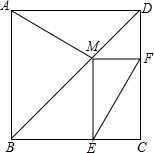 如图,在边长为7的正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.请解答下列问题:
如图,在边长为7的正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.请解答下列问题:(1)试探究线段AM与EF的大小关系并说明理由;
(2)若BE=4,求AM的长.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)可先证明四边形APMQ是矩形,再证明△ABM≌△CBM,可证得AM=CM=EF;
(2)先求得EC,由勾股定理可求得EF,由(1)可得AM的长.
(2)先求得EC,由勾股定理可求得EF,由(1)可得AM的长.
解答:解:(1)AM=EF,
理由:∵ME∥CD,MF∥BC,∠C=90°,
∴四边形CEMF是矩形,
∴CM=EF,
连接MC,
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS),
∴AM=CM=EF;
(2)∵BC=7,BE=4,
∴EC=3,
在Rt△EFC中,可求得EF=5,
∴AM=EF=5.
理由:∵ME∥CD,MF∥BC,∠C=90°,
∴四边形CEMF是矩形,
∴CM=EF,
连接MC,

在△ABM和△CBM中,
|
∴△ABM≌△CBM(SAS),
∴AM=CM=EF;
(2)∵BC=7,BE=4,
∴EC=3,
在Rt△EFC中,可求得EF=5,
∴AM=EF=5.
点评:本题主要考查正方形的性质及矩形的判定,先判定出四边形CEMF是矩形得到CM=EF是解题的关键.

练习册系列答案
相关题目
 如图中的同旁内的角共有( )
如图中的同旁内的角共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
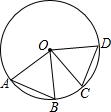 已知,如图,∠AOB=∠COD,下列结论不一定成立的是( )
已知,如图,∠AOB=∠COD,下列结论不一定成立的是( )| A、AB=CD | ||||
B、
| ||||
| C、△AOB≌△COD | ||||
| D、△AOB、△COD都是等边三角形 |
 请在方格纸上画出与AB、CD垂直的线段,并用字母表示.
请在方格纸上画出与AB、CD垂直的线段,并用字母表示.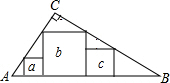 如图,在Rt△ABC中(∠C=90°)放置边长分别为a、b、c的三个正方形,则a、b、c三者之间的数量关系为
如图,在Rt△ABC中(∠C=90°)放置边长分别为a、b、c的三个正方形,则a、b、c三者之间的数量关系为 如图,直线BD上有一点C,则:
如图,直线BD上有一点C,则: 如图所示,在图中:
如图所示,在图中: 分别指出如图中的同位角、内错角、同旁内角.
分别指出如图中的同位角、内错角、同旁内角.