题目内容
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交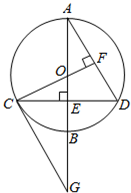 AD于点F,且CF⊥AD.
AD于点F,且CF⊥AD.(1)试问:CG是⊙O的切线吗?说明理由;
(2)请证明:E是OB的中点;
(3)若AB=8,求CD的长.
分析:(1)已知点C在圆上,根据平行线的性质可得∠FCG=90°,即OC⊥CG;故CG是⊙O的切线.
(2)方法比较多,应通过等边三角形的性质或三角形全等的思路来考虑;
(3)Rt△OCE中,有三角函数的定义,可得CE=OE×cot30°,故代入OE=2可得CE的长.
(2)方法比较多,应通过等边三角形的性质或三角形全等的思路来考虑;
(3)Rt△OCE中,有三角函数的定义,可得CE=OE×cot30°,故代入OE=2可得CE的长.
解答:(1)解:CG是⊙O的切线.理由如下:
∵CG∥AD,
∵CF⊥AD,
∴OC⊥CG.
∴CG是⊙O的切线;
(2)证明:
第一种方法:连接AC,如图,(2分)
∵CF⊥AD,AE⊥CD且CF,AE过圆心O,
∴
=
,
=
.
∴AC=AD=CD.
∴△ACD是等边三角形.(3分)
∴∠D=60°.
∴∠FCD=30°.(4分)
在Rt△COE中,
∴OE=
OB.
∴点E为OB的中点.(5分)
第二种方法:连接BD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°.
又∵∠AFO=90°,
∴∠ADB=∠AFO,∴CF∥BD.
∴△BDE∽△OCE.(3分)
=
.
∵AE⊥CD,且AE过圆心O,
∴CE=DE.(4分)
∴BE=OE.
∴点E为OB的中点.(5分)
(3)解:∵AB=8,
∴OC=
AB=4.
又∵BE=OE,
∴OE=2.(6)
∴CE=OE×cot30°=2
.(7分)
∵AB⊥CD,
∴CD=2CE=4
.(8分)
∵CG∥AD,
∵CF⊥AD,
∴OC⊥CG.
∴CG是⊙O的切线;
(2)证明:
第一种方法:连接AC,如图,(2分)

∵CF⊥AD,AE⊥CD且CF,AE过圆心O,
∴
 |
| AC |
 |
| AD |
 |
| AC |
 |
| CD |
∴AC=AD=CD.
∴△ACD是等边三角形.(3分)
∴∠D=60°.
∴∠FCD=30°.(4分)
在Rt△COE中,
∴OE=
| 1 |
| 2 |
∴点E为OB的中点.(5分)
第二种方法:连接BD,如图,
∵AB为⊙O的直径,

∴∠ADB=90°.
又∵∠AFO=90°,
∴∠ADB=∠AFO,∴CF∥BD.
∴△BDE∽△OCE.(3分)
| BE |
| OE |
| DE |
| CE |
∵AE⊥CD,且AE过圆心O,
∴CE=DE.(4分)
∴BE=OE.
∴点E为OB的中点.(5分)
(3)解:∵AB=8,
∴OC=
| 1 |
| 2 |
又∵BE=OE,
∴OE=2.(6)
∴CE=OE×cot30°=2
| 3 |
∵AB⊥CD,
∴CD=2CE=4
| 3 |
点评:本题考查常见的几何题型,包括切线的判定,线段等量关系的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )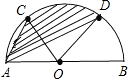 如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和 22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有
22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有 如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )
如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( ) (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )