题目内容
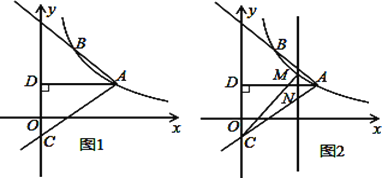
【题目】如图1,抛物线![]() 平移后过点A(8,,0)和原点,顶点为B,对称轴与
平移后过点A(8,,0)和原点,顶点为B,对称轴与![]() 轴相交于点C,与原抛物线相交于点D.
轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式并直接写出阴影部分的面积![]() ;
;
(2)如图2,直线AB与![]() 轴相交于点P,点M为线段OA上一动点,
轴相交于点P,点M为线段OA上一动点,![]() 为直角,边MN与AP相交于点N,设
为直角,边MN与AP相交于点N,设![]() ,试探求:
,试探求:
①![]() 为何值时
为何值时![]() 为等腰三角形;
为等腰三角形;
②![]() 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.


【答案】(1)平移后抛物线的解析式![]() ,
,![]() = 12;(2)①
= 12;(2)①![]() ,②当
,②当![]() =3时,PN取最小值为
=3时,PN取最小值为![]() .
.
【解析】
(1)设平移后抛物线的解析式y=![]() x2+bx,将点A(8,0)代入,根据待定系数法即可求得平移后抛物线的解析式,再根据割补法由三角形面积公式即可求解;
x2+bx,将点A(8,0)代入,根据待定系数法即可求得平移后抛物线的解析式,再根据割补法由三角形面积公式即可求解;
(2)作NQ垂直于x轴于点Q,
①分当MN=AN时,当AM=AN时,当MN=MA时,三种情况讨论可得△MAN为等腰三角形时t的值;
②由MN所在直线方程为y=![]() ,与直线AB的解析式y=﹣x+6联立,得xN的最小值为6,此时t=3,PN取最小值为
,与直线AB的解析式y=﹣x+6联立,得xN的最小值为6,此时t=3,PN取最小值为![]() .
.
(1)设平移后抛物线的解析式![]() ,
,
将点A(8,,0)代入,得![]() =
=![]() ,
,
所以顶点B(4,3),
所以S阴影=OCCB=12;
(2)设直线AB解析式为y=mx+n,将A(8,0)、B(4,3)分别代入得
![]() ,解得:
,解得: ,
,
所以直线AB的解析式为![]() ,作NQ垂直于x轴于点Q,
,作NQ垂直于x轴于点Q,
①当MN=AN时, N点的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
由三角形NQM和三角形MOP相似可知![]() ,得
,得![]() ,解得
,解得![]() (舍去).
(舍去).
当AM=AN时,AN=![]() ,由三角形ANQ和三角形APO相似可知
,由三角形ANQ和三角形APO相似可知![]() ,
,![]() ,MQ=
,MQ=![]() ,
,
由三角形NQM和三角形MOP相似可知![]() 得:
得:![]() ,
,
解得:
t=12(舍去);
当MN=MA时,![]() 故
故![]() 是钝角,显然不成立,
是钝角,显然不成立,
故![]() ;
;
②由MN所在直线方程为y=![]() ,与直线AB的解析式y=﹣x+6联立,
,与直线AB的解析式y=﹣x+6联立,
得点N的横坐标为XN=![]() ,即t2﹣xNt+36﹣xN=0,
,即t2﹣xNt+36﹣xN=0,
由判别式△=x2N﹣4(36﹣![]() )≥0,得xN≥6或xN≤﹣14,
)≥0,得xN≥6或xN≤﹣14,
又因为0<xN<8,
所以xN的最小值为6,此时t=3,
当t=3时,N的坐标为(6,),此时PN取最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案