题目内容
5.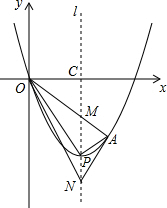 如图,顶点为P(2,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,
如图,顶点为P(2,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,(1)求该二次函数的关系式.
(2)若点A的坐标是(3,-3),求△OAP的面积.
(3)当点A在对称轴l右侧的二次函数图象上运动时,l上有一点N,且点M、N关于点P对称,试证明:∠ANM=∠ONM.
分析 (1)由于已知抛物线顶点坐标,则可设顶点式y=a(x-2)2-4,然后把原点坐标代入求出a即可得到二次函数解析式;
(2)先利用待定系数法求出直线OA的解析式为y=-x,则确定M(2,-2),则MP=2,由于△OPM和△APM共底边PM,且PM边上的高的和为3,于是可利用S△OAP=S△OPM+S△APM进行计算;
(3)过点A作AB⊥x轴于点B,AH⊥l于点H,l与x轴交于点C,如图,根据二次函数图象上点的坐标特征,设 A(m,m2-4m),则 H(2,m2-4m),B(m,0),C(2,0),通过证明△OCM∽△OBA,可求出CM=-2m+8,得到M(2,2m-8),再利用点M、N关于点P对称得到N(2,-2m),接着计算出$\frac{OC}{NC}$=$\frac{1}{m}$,$\frac{AH}{NH}$=$\frac{1}{m}$,即有$\frac{OC}{NC}$=$\frac{AH}{NH}$,根据相似三角形的判定方法得到△OCN∽△AHN,然后根据相似三角形的性质即可得到结论.
解答 (1)解:设二次函数的关系式为y=a(x-2)2-4,
∵二次函数图象经过原点(0,0),
∴0=(0-2)2-4,解得a=1,
∴二次函数解析式为y=(x-2)2-4,即y=x2-4x;
(2)解:设直线OA的解析式为y=kx,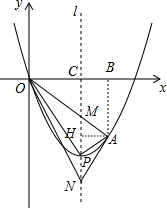
将A(3,-3)代入得-3=3k,解得k=-1,
∴直线OA的解析式为y=-x,
当x=2代入y=-x=-2,
∴M(2,-2),
∴MP=-2+4=2,
∴S△OAP=S△OPM+S△APM=$\frac{1}{2}$×3×2=3;
(3)证明:过点A作AB⊥x轴于点B,AH⊥l于点H,l与x轴交于点C,如图,
设 A(m,m2-4m),则 H(2,m2-4m),B(m,0),C(2,0),
∵CM∥AB,
∴△OCM∽△OBA,
∴$\frac{CM}{AB}$=$\frac{OC}{OB}$,即$\frac{CM}{-{m}^{2}+4m}$=$\frac{2}{m}$,解得CM=-2m+8,
∴M(2,2m-8),
∴MP=2m-8+4=2m-4,
∵点M、N关于点P对称,
∴PN=MP=2m-4,
∴N(2,-2m),
∵OC=2,CN=2m,AH=m-2,NH=m2-2m,
∴$\frac{OC}{NC}$=$\frac{1}{m}$,$\frac{AH}{NH}$=$\frac{m-2}{{m}^{2}-2m}$=$\frac{1}{m}$
∴$\frac{OC}{NC}$=$\frac{AH}{NH}$,
而∠OCN=∠AHN,
∴△OCN∽△AHN,
∴∠ONC=∠ANH,
即∠ANM=∠ONM.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求二次函数的解析式;理解坐标与图形性质;会利用相似三角形的判定与性质证明角相等的问题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案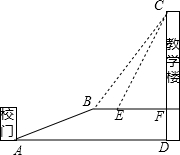 重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.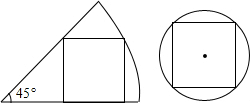 一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是5:4.
一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是5:4.