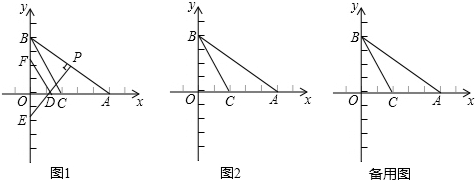
题目内容
在△ABC中,BD,CE是它的两条角平分线,且BD,CE相交于点M,MN⊥BC于点N.将∠MBN记为∠1,∠MCN记为∠2,∠CMN记为∠3.

(1)如图1,若∠A=110°,∠BEC=130°,则∠2=°,∠3-∠1=°;
(2)如图2,猜想∠3-∠1与∠A的数量关系,并证明你的结论;
(3)若∠BEC=α,∠BDC=β,用含α和β的代数式表示∠3-∠1的度数.(直接写出结果即可)

(1)如图1,若∠A=110°,∠BEC=130°,则∠2=°,∠3-∠1=°;
(2)如图2,猜想∠3-∠1与∠A的数量关系,并证明你的结论;
(3)若∠BEC=α,∠BDC=β,用含α和β的代数式表示∠3-∠1的度数.(直接写出结果即可)
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACE=∠BEC-∠A,再根据角平分线的定义可得∠2=∠ACE;根据角平分线的定义求出∠ACB,再根据三角形的内角和定理求出∠ABC,然后求出∠1,根据直角三角形两锐角互余求出∠3,然后相减即可得解;
(2)根据角平分线的定义可得∠1=
∠ABC,∠2=
∠ACB,再根据直角三角形两锐角互余表示出∠3,然后表示出∠3-∠1=90°-
∠ACB-
∠ABC,再根据三角形的内角和定理可得∠ACB+∠ABC=180°-∠A,然后代入整理即可得解;
(3)在△BCE和△BCD中,根据三角形内角和定理列式整理得到∠1+∠2,再根据三角形的内角和定理和角平分线的定义用∠A表示出∠1+∠2,然后根据∠3-∠1=
∠A整理即可得解.
(2)根据角平分线的定义可得∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)在△BCE和△BCD中,根据三角形内角和定理列式整理得到∠1+∠2,再根据三角形的内角和定理和角平分线的定义用∠A表示出∠1+∠2,然后根据∠3-∠1=
| 1 |
| 2 |
解答:(1)解:在△ACE中,∠ACE=∠BEC-∠A
=130°-110°
=20°,
∵CE平分∠ACE,
∴∠2=∠ACE=20°,
∠ACB=2∠2=2×20°=40°,
在△ABC中,∠ABC=180°-∠A-∠ACB=180°-110°-40°=30°,
∵BD平分∠ABC,
∴∠1=
∠ABC=
×30°=15°,
∵MN⊥BC,
∴∠3=90°-∠2=90°-20°=70°,
∴∠3-∠1=70°-15°=55°,
故答案为:20,55;
(2)∠3-∠1与∠A的数量关系是:∠3-∠1=
∠A.
证明:∵在△ABC中,BD,CE是它的两条角平分线,
∴∠1=
∠ABC,∠2=
∠ACB,
∵MN⊥BC于点N,
∴∠MNC=90°,
∴在△MNC中,∠3=90°-∠2,
∴∠3-∠1=90°-∠2-∠1,
=90°-
∠ACB-
∠ABC,
=90°-
(∠ACB+∠ABC),
∵在△ABC中,∠ACB+∠ABC=180°-∠A,
∴∠3-∠1=90°-
(180°-∠A),
=
∠A;
(3)解:∵BD,CE是△ABC的两条角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
在△BCE和△BCD中,∠1+2∠2+β=180°,
∠2+2∠1+α=180°,
∴∠1+∠2=120°-
,
∵∠1+∠2=
(∠ACB+∠ABC)=
(180°-∠A),
∴120°-
=
(180°-∠A),
整理得,
∠A=
-30°,
∴∠3-∠1=
-30°.
=130°-110°
=20°,
∵CE平分∠ACE,
∴∠2=∠ACE=20°,
∠ACB=2∠2=2×20°=40°,
在△ABC中,∠ABC=180°-∠A-∠ACB=180°-110°-40°=30°,
∵BD平分∠ABC,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵MN⊥BC,
∴∠3=90°-∠2=90°-20°=70°,
∴∠3-∠1=70°-15°=55°,
故答案为:20,55;
(2)∠3-∠1与∠A的数量关系是:∠3-∠1=
| 1 |
| 2 |
证明:∵在△ABC中,BD,CE是它的两条角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵MN⊥BC于点N,
∴∠MNC=90°,
∴在△MNC中,∠3=90°-∠2,
∴∠3-∠1=90°-∠2-∠1,
=90°-
| 1 |
| 2 |
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
∵在△ABC中,∠ACB+∠ABC=180°-∠A,
∴∠3-∠1=90°-
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)解:∵BD,CE是△ABC的两条角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
在△BCE和△BCD中,∠1+2∠2+β=180°,
∠2+2∠1+α=180°,
∴∠1+∠2=120°-
| α+β |
| 3 |
∵∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴120°-
| α+β |
| 3 |
| 1 |
| 2 |
整理得,
| 1 |
| 2 |
| α+β |
| 3 |
∴∠3-∠1=
| α+β |
| 3 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a=(-3)13-(-3)14,b=(-0.6)12-(-0.6)14,c=(-1.5)11-(-1.5)13,则下列有关a、b、c的大
小关系,何者正确?( )
小关系,何者正确?( )
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>b>a |
 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B. 如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.你能判断DF与AB的位置关系吗?请说明理由.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.你能判断DF与AB的位置关系吗?请说明理由. 如图,在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=2:3,BD平分∠ABC,点F在BC上,∠CDF=30°,∠ABD=35°.
如图,在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=2:3,BD平分∠ABC,点F在BC上,∠CDF=30°,∠ABD=35°.