题目内容
4.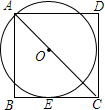 如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E.
如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E.(1)求证:CD是⊙O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.
分析 (1)首先连接OE,并过点O作OF⊥CD,由OA长为半径的⊙O与BC相切于点E,可得OE=OA,OE⊥BC,然后由AC为正方形ABCD的对角线,根据角平分线的性质,可证得OF=OE=OA,即可判定CD是⊙O的切线;
(2)由正方形ABCD的边长为10,可求得其对角线的长,然后由设OA=r,可得OE=EC=r,由勾股定理求得OC=$\sqrt{2}$r,则可得方程r+$\sqrt{2}$r=10$\sqrt{2}$,继而求得答案.
解答 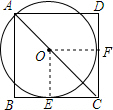 (1)证明:连接OE,并过点O作OF⊥CD.
(1)证明:连接OE,并过点O作OF⊥CD.
∵BC切⊙O于点E,
∴OE⊥BC,OE=OA,
又∵AC为正方形ABCD的对角线,
∴∠ACB=∠ACD,
∴OF=OE=OA,
即:CD是⊙O的切线.
(2)解:∵正方形ABCD的边长为10,
∴AB=BC=10,∠B=90°,∠ACB=45°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10$\sqrt{2}$,
∵OE⊥BC,
∴OE=EC,
设OA=r,则OE=EC=r,
∴OC=$\sqrt{O{E}^{2}+E{C}^{2}}$=$\sqrt{2}$r,
∵OA+OC=AC,
∴r+$\sqrt{2}$r=10$\sqrt{2}$,
解得:r=20-10$\sqrt{2}$.
∴⊙O的半径为:20-10$\sqrt{2}$.
点评 此题考查了切线的判定、正方形的性质、角平分线的性质以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
15.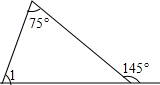 如图,∠1的度数是( )
如图,∠1的度数是( )
 如图,∠1的度数是( )
如图,∠1的度数是( )| A. | 75° | B. | 60° | C. | 85° | D. | 70° |
12.计算:(-5)×(-4)×(-6)×(-5)的结果是( )
| A. | 600 | B. | -600 | C. | 20 | D. | -20 |
9.如图是一个简单的数值运算程序,当输出y的值为-1时,则输入x的值为( )


| A. | 1 | B. | 5 | C. | -1 | D. | ±1 |
16.大纵湖自古为盐城名胜,纵湖秋色列入盐城新十景之一.她以宁静致远的意境、恬淡秀美的风光、清雅绮丽的魅力吸引着众多游客前来观光.今年“十一”黄金周期间,盐都区大纵湖旅游风景区在七天假期中每天旅游人数变化如下(正数表示比前一天多的人数,负数表示比前一天少的人数).若9月30日游客人数为0.8万人(单位:万人)
(1)10月2日的游客人数是多少人?
(2)请判断7天内游客最多的人数是哪天?最少的人数是哪天?
(3)求这一次黄金周期间游客在该地的总人数.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +0.6 | +0.4 | +0.2 | -0.5 | -0.8 | +0.2 | -0.3 |
(2)请判断7天内游客最多的人数是哪天?最少的人数是哪天?
(3)求这一次黄金周期间游客在该地的总人数.